Ecuaciones de Segundo Grado - PAES M1

Este resumen corresponde al Eje Temático Álgebra y funciones en la unidad temática Ecuaciones de segundo grado, la que se describe como:

• Resolución de ecuaciones de segundo grado.
• Casos en los cuales la ecuación cuadrática tiene dos, una o no tiene solución real.
• Problemas que involucren ecuaciones cuadráticas en diversos contextos.

¿Qué es una ecuación de segundo grado?

Una ecuación de segundo grado en una variable es una ecuación que puede escribirse de la forma $ax^2 + bx + c = 0$, donde $a$, $b$ y $c$ son números reales y $a \neq 0$.
Una ecuación de segundo grado en una variable posee una incógnita cuyo mayor exponente es 2. Este tipo de ecuaciones también se conoce como ecuación cuadrática.

Importante: Una raíz de una ecuación es una solución de la ecuación. Resolver una ecuación de segundo grado con una incógnita es encontrar el valor o los valores que debe tomar la incógnita para que la desigualdad sea verdadera. Las ecuaciones cuadráticas pueden tener cero, una o dos soluciones reales.

Resolver ecuaciones cuadráticas

Existen diversos métodos para resolver una ecuación cuadrática: haciendo una representación gráfica, factorizando, calculando raíces cuadradas, completando cuadrados o aplicando la fórmula cuadrática.

Resolver ecuaciones cuadráticas usando el método gráfico

Este método consiste en encontrar las intersecciones con el eje $x$ de la función relacionada $y = ax^2 + bx + c$. Este método se debe usar cuando las soluciones son números enteros o cuando las soluciones aproximadas son útiles.

Por ejemplo, para encontrar las soluciones de $x^2-4x+3=0$ puedes representar gráficamente la función $y=x^2-4x+3$ en el plano cartesiano, obteniendo el siguiente gráfico.

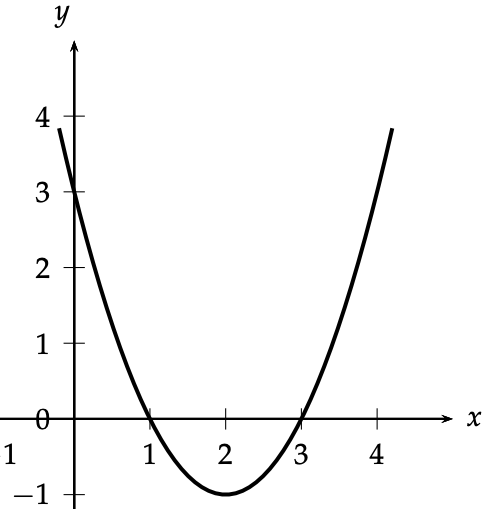
Las intersecciones con el eje $x$ son 1 y 3, por lo que las soluciones o raíces de $x^2-4x+3=0$ son $x=1$ y $x=3$.

Importante: Al encontrar las intersecciones con el eje $x$ de la función relacionada $y = ax^2 + bx + c$, el gráfico puede cortar al eje $x$ en dos, uno o ningún punto.
$\star$ Si el gráfico corta al eje $x$ en dos puntos, la ecuación $ax^2 + bx + c=0$ tiene dos soluciones reales y distintas.
$\star$ Si el gráfico corta al eje $x$ en un punto, la ecuación $ax^2 + bx + c=0$ tiene dos soluciones reales e iguales (una solución).
$\star$ Si el gráfico no corta al eje $x$, la ecuación $ax^2 + bx + c=0$ no tiene soluciones reales.

En el ejemplo anterior, dado que el valor de la función es cero cuando $x =1$ y cuando $x = 3$, los números 1 y 3 también se llaman ceros de la función. Un cero de una función $f$ es un valor de $x$ para el cual $f(x) = 0$.

En términos generales, si un número real $k$ es un cero de la función $f(x)=ax^2 +bx+c$, entonces $k$ es una intersección con el eje $x$ de la gráfica de la función, y $k$ también es una raíz de la ecuación $ax^2 + bx + c = 0$.

Resolver ecuaciones cuadráticas factorizando

Cuando el lado izquierdo de la ecuación $ax^2 + bx + c = 0$ es factorizable, puedes resolver la ecuación usando la propiedad del producto cero. Este método se debe usar cuando se puedan factorizar fácilmente las ecuaciones cuadráticas.

Propiedad del producto cero
Si el producto de dos expresiones es cero, entonces una o ambas de las expresiones es igual a cero.
Algebraicamente, si $P$ y $Q$ son expresiones y $PQ=0$, entonces $P = 0$ o $Q = 0$.

Por ejemplo, para encontrar las soluciones de $x^2-4x+3=0$ puedes factorizar $x^2-4x+3$ como $(x-3)(x-1)$, obteniendo la ecuación equivalente $(x-3)(x-1)=0$. Aplicando la propiedad del producto cero, se sabe que $x-3=0$ o $x-1=0$, concluyendo que $x=3$ o $x=1$.

Resolver ecuaciones cuadráticas calculando raíces cuadradas

Este método se debe usar cuando la ecuación puede ser escrita de la forma $u^2 = d$, donde $u$ es una expresión algebraica. Al escribir la ecuación en la forma $u^2 = d$, ésta se resuelve sacando la raíz cuadrada de cada lado de la igualdad.

Por ejemplo, la ecuación $3x^2 +9=0$ se puede resolver reescribiéndola como $3x^2=-9$ al restar 9 a cada lado de la igualdad. Luego, dividiendo por 3 a ambos lados, se obtiene $x^2=-3$. Como el cuadrado de un número real no puede ser negativo, la ecuación no tiene una solución real.

Otro ejemplo es resolver la ecuación $4x^2-31=49$. Al sumar 31 a cada lado de la igualdad, se obtiene $4x^2=80$. Luego, dividiendo por 4 a ambos lados, se obtiene $x^2=20$. Finalmente, se concluye que las soluciones son $x=\sqrt{20}$ y $x=-\sqrt{20}$.

Las soluciones de $x^2-16x + 64 = 100$ también pueden ser encontradas empleando este método, puesto que $x^2-16x + 64$ es igual que $(x-8)^2$. Así, $x^2-16x + 64 = 100$ equivale a $(x-8)^2 = 100$. Al calcular la raíz cuadrada a ambos lados de la igualdad, $\sqrt{(x-8)^2}=|x-8|$ y $\sqrt{100}=10$. De la igualdad $|x-8|=10$ se concluye que $x=18$ y $x=-2$.

Resolver ecuaciones cuadráticas completando cuadrados

En el ejemplo anterior, la expresión $x^2-16x + 64$ es un trinomio cuadrado perfecto porque es igual al cuadrado de binomio $(x-8)^2$.

Importante: A veces necesitas sumar un término a una expresión $x^2+bx$ para convertirla en un trinomio cuadrado perfecto. Este proceso se llama completar el cuadrado.
Para completar el cuadrado de la expresión $x^2+bx$, debes sumar $\left(\frac{b}{2}\right)^2$ como se muestra a continuación:

$$\begin{aligned} x^2 + bx + \left(\frac{b}{2}\right)^2 &= \left(x + \frac{b}{2}\right)\left(x + \frac{b}{2}\right) \\ &= \left(x + \frac{b}{2}\right)^2 \end{aligned}$$

Por ejemplo, para encontrar el valor de $c$ que hace que $x^2 + 14x + c$ sea un trinomio cuadrado perfecto, debes calcular la mitad de 14 y elevar el resultado al cuadrado. Así, $c=\left(\dfrac{14}{2}\right)^2=7^2=49$. Entonces, $x^2 + 14x + 49 = (x + 7)(x + 7) = (x + 7)^2$.

Importante: El método de completar el cuadrado puede usarse para cualquier ecuación cuadrática $ax^2 + bx + c = 0$, pero es más fácil aplicarlo cuando $a = 1$ y $b$ es un número par. Cuando completes el cuadrado como parte de resolver una ecuación, deberás sumar el mismo número a ambos lados de la ecuación.

Por ejemplo, al resolver $x^2-10x + 7 = 0$ completando el cuadrado, reescribes la ecuación restando 7 a ambos lados de la igualdad: $x^2-10x=-7$. Sumas a ambos lados $\left(\dfrac{-10}{2}\right)^2=25$ y obtienes $x^2-10x+25=-7+25$. Con esto puedes reescribir la igualdad como $(x-5)^2=18$ y aplicando raíz cuadrada a ambos lados de la igualdad se obtiene que $x=5+\sqrt{18}$ y $x=5-\sqrt{18}$.

Resolver ecuaciones cuadráticas usando la fórmula cuadrática

Para cualquier ecuación cuadrática, al completar el cuadrado para la ecuación general $ax^2 + bx + c = 0$ se obtiene la fórmula para obtener las soluciones de la ecuación. Esta fórmula se denomina fórmula cuadrática.

Importante: Sean $a$, $b$ y $c$ números reales tal que $a \neq 0$. Las soluciones de la ecuación cuadrática $ax^2+bx+c=0$ son $x=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

Por ejemplo, para encontrar las soluciones de $x^2-4x+3=0$ usando la fórmula cuadrática debes identificar los coeficientes $a=1$, $b=-4$ y $c=3$. Reemplazando en la fórmula cuadrática se obtiene:

$$\begin{aligned} x &= \dfrac{-(-4)\pm \sqrt{(-4)^2-4\cdot 1\cdot 3}}{2\cdot 1} \\ &= \dfrac{4\pm \sqrt{16-12}}{2} \\ &= \dfrac{4\pm \sqrt{4}}{2} \\ &= \dfrac{4\pm 2}{2} \end{aligned}$$

Entonces, las soluciones de la ecuación $x^2-4x+3=0$ son $x=\dfrac{4+2}{2}=\dfrac{6}{2}=3$ y $x=\dfrac{4-2}{2}=\dfrac{2}{2}=1$.

Importante: En la fórmula cuadrática, la expresión $b^2-4ac$ se llama el discriminante de la ecuación asociada $ax^2 + bx + c = 0$.
$\star$ Si el discriminante es mayor que cero, la ecuación tiene dos soluciones distintas y reales.
$\star$ Si el discriminante es igual que cero, la ecuación tiene dos soluciones iguales y reales (una solución).
$\star$ Si el discriminante es menor que cero, la ecuación tiene dos soluciones que no son reales.