Expresiones algebraicas - PAES M1

Este resumen corresponde al Eje Temático Álgebra y funciones en la unidad temática Expresiones algebraicas la que se describe como:

• Productos notables.
• Factorizaciones de expresiones algebraicas.
• Operatoria con expresiones algebraicas.
• Problemas que involucren expresiones algebraicas en diversos contextos.

¿Qué es una expresión algebraica?

Una expresión algebraica es un conjunto de números y letras relacionados entre sí por los signos de las operaciones básicas (adición y sustracción). Por ejemplo, $2x-xm+6z^2$ es una expresión algebraica que consta de tres términos algebraicos.

• $3x + 2$
• $a^2 - b^2$
• $5(x - 4)^2$

Un término algebraico posee un coeficiente numérico (si es 1, no es necesario escribirlo y queda tácito) y un factor literal (una o más letras). En el ejemplo anterior, los términos algebraicos son $2x$, $\; -xm\;$ y $\;6z^2$.

El grado de un término algebraico es la suma de los exponentes de los factores literales que lo componen. Por ejemplo, el grado de $x^2$ es 2 y el grado de $x^2y^3$ es 5.

El grado de una expresión algebraica que contiene un único tipo de factor literal, es el exponente mayor de esta letra en la expresión. Por ejemplo, la expresión algebraica $x^2-3x+1$ tiene grado 2, puesto que el factor literal $x$ tiene como exponente mayor a 2.

El grado de una expresión algebraica que tiene más de un tipo de factor literal, es igual al grado del término algebraico de mayor grado que contiene la expresión. Por ejemplo, la expresión algebraica $x^2y^2-3xy^2+x^3$ tiene grado 4, puesto que el término $x^2y^2$ tiene el mayor grado ($2+2=4$).

Valor numérico de una expresión algebraica

El valor numérico de una expresión algebraica se encuentra sustituyendo cada letra por un número determinado. Por ejemplo:

¿Cuál es el valor de $x^2 - 2xy$, si $x=2$ e $y=-1$? (DEMRE 2007)

Para responder la pregunta anterior, debes sustituir $x=2$ e $y=-1$ en $x^2 - 2xy$:

$$2^2 - 2 \cdot 2 \cdot (-1) = 4 - (-4) = 4 + 4 = 8$$

Una expresión algebraica compuesta exactamente por:

• un término algebraico se denomina monomio.
• dos términos algebraicos se denomina binomio.
• tres términos algebraicos se denomina trinomio.
• cuatro o más términos algebraicos se denomina polinomio.

Reducción de términos semejantes

Dos o más términos algebraicos son semejantes si poseen el mismo factor literal. Por ejemplo, $\frac{2}{3}p^2q$ y $-5p^2q$ son términos semejantes porque ambos tienen factor literal $p^2q$.

Cuando dos o más términos algebraicos son semejantes y están dispuestos en una expresión algebraica, es posible reducirlos.

Reducir términos semejantes consiste en sumar o restar los coeficientes numéricos de los términos, conservando el factor literal que tienen en común. Por ejemplo, los términos algebraicos $5x$ y $-3x$ son semejantes, por lo tanto, la expresión algebraica $5x - 3x$ es equivalente a $2x$.

Lenguaje algebraico

El lenguaje algebraico permite representar cantidades desconocidas e información expresada en lenguaje natural, además, permite generalizar relaciones entre cantidades y expresar propiedades de la matemática, gracias al uso de términos algebraicos, símbolos y/o signos de operaciones definidas.

La siguiente tabla muestra algunas frases del lenguaje natural y su traducción al lenguaje algebraico. Nota que generalmente se emplea la letra $x$, pero es posible usar cualquier otra.

$$\begin{array}{|l|c|} \hline \textbf{\text{Lenguaje natural}} & \textbf{\text{Lenguaje algebraico}} \\ \hline \text{El doble de un número} & 2x \\ \hline \text{La mitad de un número} & \dfrac{x}{2} \\ \hline \text{El triple de un número} & 3x \\ \hline \text{La tercera parte de un número} & \dfrac{x}{3} \\ \hline \text{Cuatro veces un número} & 4x \\ \hline \text{El cuadrado de un número} & x^2 \\ \hline \text{El cubo de un número} & x^3 \\ \hline \end{array}$$

Lenguaje natural	Lenguaje algebraico
El inverso aditivo de un número	$-x$
El opuesto de un número	$-x$
El inverso multiplicativo de un número	$\dfrac{1}{x}$, con $x \neq 0$
El recíproco de un número	$\dfrac{1}{x}$, con $x \neq 0$
La diferencia de dos números	$x - y$
El exceso de un número respecto de otro	$x - y$, con $x > y$
El cociente de dos números	$x : y$, con $y \neq 0$
El producto de dos números	$x \cdot y$
El antecesor de un número	$x - 1$
El sucesor de un número	$x + 1$
Un número par	$2x$, con $x \in \mathbb{Z}$
Un número impar	$2x + 1$, con $x \in \mathbb{Z}$
Un múltiplo de 5	$5x$, con $x \in \mathbb{Z}$
Dos números enteros consecutivos	$x$ y $x + 1$, con $x \in \mathbb{Z}$
Dos números pares consecutivos	$2x$ y $2x + 2$, con $x \in \mathbb{Z}$
Dos números impares consecutivos	$2x + 1$ y $2x + 3$, con $x \in \mathbb{Z}$
La distancia entre dos números	$|x - y|$
Un número positivo	$x > 0$
Un número negativo	$x < 0$
Un número a lo más igual que diez	$x \leq 10$
Un número a lo menos igual que diez	$x \geq 10$

Factorización de expresiones algebraicas

Factorizar una expresión algebraica consiste en representarla como una multiplicación de otros términos y/o expresiones algebraicas. Los factores de una expresión algebraica son divisores de ésta.

Nota que no todas las expresiones algebraicas se pueden factorizar a partir de otros términos y/o expresiones algebraicas.

Cuando el factor común es un monomio

Cuando una expresión algebraica está conformada por términos que poseen un factor en común (numérico o un término algebraico), es posible aplicar la propiedad distributiva de la multiplicación sobre la adición para factorizar la expresión original.

Por ejemplo, es posible factorizar la expresión algebraica $5ab^2 - 10ab$ por el término común $5ab$. Aplicando la propiedad distributiva de la multiplicación sobre la adición se obtiene que:

$$5ab^2 - 10ab = 5ab \cdot (b - 2)$$

¿Cómo reconocer el factor común monomio de una expresión algebraica?
Primero, debes determinar el mínimo común múltiplo entre los coeficientes numéricos de cada término de la expresión algebraica. Luego, debes identificar la letra o las letras que se repiten en cada término de la expresión algebraica, considerando el menor exponente. El factor común monomio estará formado por el producto de los datos encontrados en estos pasos previos.

Cuando el factor común es un binomio

Este caso corresponde a la aplicación de la misma lógica descrita anteriormente, pero el factor común corresponde a un binomio.

Por ejemplo, es posible factorizar la expresión algebraica $2(x + y) - 3a(x + y)$ por el término común $(x + y)$. Aplicando la propiedad distributiva de la multiplicación sobre la adición se obtiene que:

$$2(x + y) - 3a(x + y) = (x + y) \cdot (2 - 3a)$$

Factorización por agrupación

Cuando una expresión algebraica no presenta un factor común, es posible verificar si existen grupos de términos que posean un factor común, de modo que se factorice la expresión por partes. En algunas ocasiones, la factorización por agrupación te permite encontrar factores de la expresión algebraica que originalmente no eran evidentes.

Por ejemplo, es posible factorizar la expresión algebraica $mx - ny + nx - my$ agrupando los términos $mx$ y $nx$ porque tienen el factor común $x$ y agrupando los términos $-ny$ y $-my$ porque tienen el factor común $-y$:

$$mx - ny + nx - my = mx + nx - my - ny = x(m + n) - y(m + n)$$

Luego, es posible factorizar $x(m + n) - y(m + n)$ por el factor común $(m + n)$, por lo que se concluye:

$$mx - ny + nx - my = x(m + n) - y(m + n) = (m + n) \cdot (x - y)$$

Factorizando un trinomio cuadrado perfecto

Se denomina trinomio cuadrado perfecto a toda expresión algebraica que puede ser representada como un binomio al cuadrado.

Por ejemplo, la expresión algebraica $x^2+6x+9$ es un trinomio cuadrado perfecto porque puede ser representada como $(x+3)^2$, es decir, la factorización de $x^2+6x+9$ es $(x+3)\cdot(x+3)$.

En términos generales, se cumple que:

$x^2+2xy+y^2 = (x+y)\cdot(x+y) = (x+y)^2$

$x^2-2xy+y^2 = (x-y)\cdot(x-y) = (x-y)^2$

¿Cómo reconocer un trinomio cuadrado perfecto?
Primero, debes ordenar los términos del trinomio respecto de una letra y su exponente. Luego, debes comprobar si el primer y último término pueden escribirse como una sola potencia de exponente 2. Finalmente, debes verificar si el término central es equivalente al doble del producto de las bases de las potencias obtenidas en el paso anterior.

Factorizando una diferencia de cuadrados

Una diferencia de cuadrados, en el contexto de las expresiones algebraicas, corresponde a una resta de dos términos algebraicos que están al cuadrado. Al factorizar una diferencia de cuadrados se obtiene la multiplicación de una suma de dos términos y una diferencia de estos mismos términos. Cada término involucrado en esta suma y esta diferencia cumple que al cuadrado es equivalente al valor absoluto de uno de los términos presentes en la expresión original.

En términos generales, se cumple que:

$x^2 - y^2 = (x+y)\cdot(x-y)$

Factorizando un trinomio de la forma $x^2 + bx + c$

Un trinomio de la forma $x^2 + bx + c$, con $b$ y $c$ números enteros distintos que $0$, generalmente se puede factorizar como el producto de dos binomios. Para ello, debes encontrar dos números enteros que multiplicados den $c$ y sumados den $b$.

Sean $r$ y $s$ dos números enteros tales que $r \cdot s = c$ y $r + s = b$. Entonces se cumple que:

$x^2 + bx + c = (x + r)(x + s)$

En términos de los números enteros $r$ y $s$, se tiene:

$x^2 + (r + s)x + (r \cdot s) = (x + r)(x + s)$

¿Cómo reconocer los signos de los números enteros $r$ y $s$?

• Si $c > 0$, entonces $r$ y $s$ tendrán el mismo signo.
• Si $c < 0$, entonces $r$ y $s$ tendrán diferente signo.
• Si $c > 0$ y $b > 0$, entonces $r$ y $s$ serán positivos.
• Si $c > 0$ y $b < 0$, entonces $r$ y $s$ serán negativos.
• Si $c < 0$ y $b > 0$, entonces $r$ y $s$ tendrán diferente signo. Al comparar sus valores absolutos, el valor absoluto del número positivo será mayor.
• Si $c < 0$ y $b < 0$, entonces $r$ y $s$ tendrán diferente signo. Al comparar sus valores absolutos, el valor absoluto del número positivo será menor.

Factorizando un trinomio de la forma $ax^2 + bx + c$

Un trinomio de la forma $ax^2 + bx + c$, con $a$, $b$ y $c$ números enteros distintos que $0$, generalmente se puede factorizar. Para ello, debes partir verificando si $a$ es factor común de los términos del trinomio. Si es así, factorizas por $a$ y el trinomio resultante se factoriza como se explicó anteriormente.

Por ejemplo, al factorizar $2x^2 + 10x + 12$ se puede comenzar advirtiendo que 2 es factor común de los términos del trinomio, por lo que se cumple que:

$2x^2 + 10x + 12 = 2 \cdot (x^2 + 5x + 6)$

Luego, se factoriza $x^2 + 5x + 6$ como se menciona en la sección anterior, concluyendo que:

$2x^2 + 10x + 12 = 2(x + 3)(x + 2)$

Cuando los coeficientes de los términos del trinomio $ax^2 + bx + c$ no tienen un factor común, debes encontrar dos números enteros que multiplicados den $ac$ y sumados den $b$.

Sean $r$ y $s$ dos números enteros tales que $r \cdot s = ac$ y $r + s = b$. Reescribe el trinomio como $ax^2 + rx + sx + c$ y factoriza por agrupación.

Por ejemplo, al factorizar $2x^2 + 11x + 5$ se deben encontrar dos números $r$ y $s$ tales que $r \cdot s = 2 \cdot 5 = 10$ y $r + s = 11$. Estos números son 1 y 10, ya que $1 \cdot 10 = 10$ y $1 + 10 = 11$. Reescribiendo el trinomio se obtiene:

$2x^2 + 1x + 10x + 5 = x(2x + 1) + 5(2x + 1) = (2x + 1)(x + 5)$

Factorizando una suma de cubos

En términos generales, se cumple que:

$x^3 + y^3 = (x + y)(x^2 - xy + y^2)$

Factorizando una diferencia de cubos

En términos generales, se cumple que:

$x^3 - y^3 = (x - y)(x^2 + xy + y^2)$

Productos notables

Un producto notable es la factorización de una expresión algebraica, la cual se puede encontrar siguiendo reglas fijas, sin la necesidad de comprobar la igualdad entre el producto notable y la expresión algebraica.

Cuadrado de un binomio

El cuadrado de un binomio corresponde a una potencia con base igual a un binomio y con exponente 2. En términos generales, se cumple que:

$(x + y)^2 = x^2 + 2xy + y^2$

$(x - y)^2 = x^2 - 2xy + y^2$

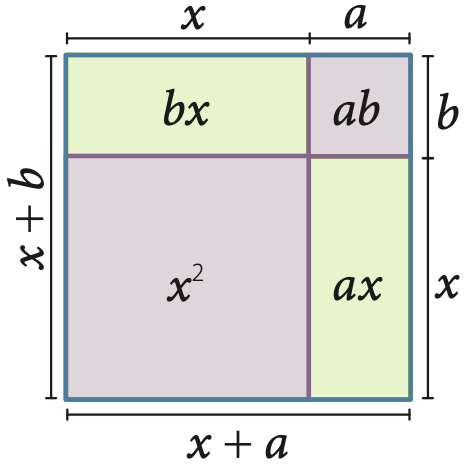
Representación gráfica del cuadrado de un binomio

$$\text{Área del cuadrado de lado } a+b=(a+b)^2=a^2+ab+ab+b^2=a^2+2ab+b^2$$

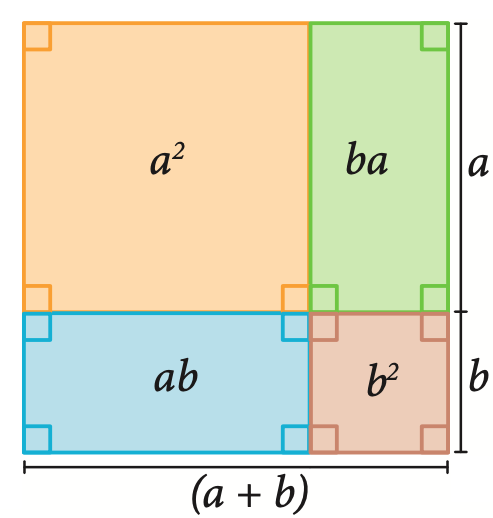
Cubo de un binomio

El cubo de un binomio corresponde a una potencia con base igual a un binomio y con exponente 3. En términos generales, se cumple que:

$$(x+y)^3=x^3+3x^2y+3xy^2+y^3$$ $$(x-y)^3=x^3-3x^2y+3xy^2-y^3$$

$$\text{Volumen del cubo de arista } a+b=(a+b)^3=a^3+3a^2b+3ab^2+b^3$$

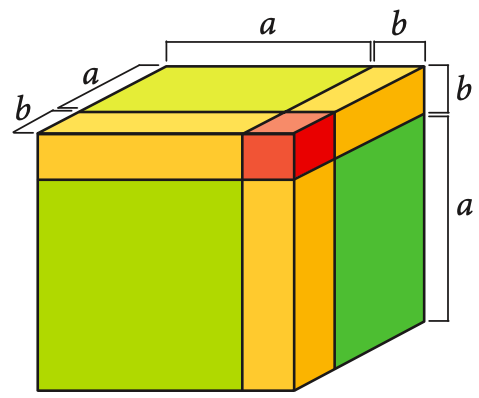
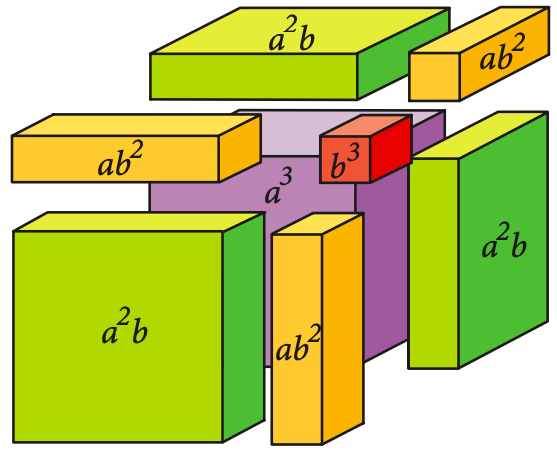
Suma por su diferencia

La suma por su diferencia corresponde a la multiplicación de la suma de dos términos algebraicos y la resta de los mismos términos. En términos generales, se cumple que:

$$(x+y)(x-y)=x^2-y^2$$

$$\text{Área del rectángulo coloreado}=(a+b)(a-b)=a^2-b^2$$

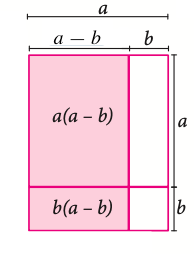
Producto de binomios con un término en común

El producto de dos binomios con un término común corresponde a la multiplicación de dos binomios de la forma $(x + a)$ y $(x + b)$, donde $x$ representa el término en común. En términos generales, se cumple que:

$$(x+a)\cdot (x+b)=x^2+(a+b)x+ab$$

$$\text{Área del rectángulo de lados } x+a \text{ y } x+b=(x+a)(x+b)=x^2+(a+b)x+ab$$

---

Expresiones algebraicas fraccionarias

Se llama expresión algebraica fraccionaria al cociente de dos expresiones algebraicas, tal que la expresión algebraica que corresponde al divisor sea distinta de 0.

Para sumar, restar, multiplicar y dividir expresiones algebraicas fraccionarias se deben seguir los mismos algoritmos usados en el conjunto de los números reales.

Una expresión algebraica fraccionaria se puede reducir o simplificar a su mínima expresión, encontrando una expresión equivalente. Para ello, primero es necesario factorizar dividendo y divisor, para luego simplificar sus factores comunes.

Por ejemplo:

$$\frac{x^2-1}{x^2-6x+5} = \frac{(x+1)(x-1)}{(x-1)(x-5)} = \frac{x+1}{x-5}$$