Proporción directa e inversa - PAES M1

Este resumen corresponde al Eje Temático Álgebra y funciones en la unidad temática Proporción directa e inversa, la que se describe como:

• Concepto de proporción directa e inversa con sus diferentes representaciones.
• Problemas que involucren proporción directa e inversa en diversos contextos.

Proporcionalidad directa

Diremos que dos magnitudes son directamente proporcionales si al aumentar una de ellas $N$ veces, entonces la otra magnitud también aumenta $N$ veces. De lo contrario, si una de las magnitudes disminuye $N$ veces, entonces la otra magnitud también disminuye $N$ veces.

Dos magnitudes son directamente proporcionales cuando, al multiplicar una de ellas por un número cualquiera, la otra queda multiplicada por el mismo número.

Como ejemplo, se han medido los volúmenes de distintos bloques de hierro y sus respectivas masas como muestra la siguiente tabla. Nota que al duplicar el volumen $V$, la masa $M$ también lo hace y al triplicar $V$, $M$ se triplica. Se puede decir que la masa de un bloque de hierro es directamente proporcional a su volumen.

$V$ (cm$^3$)	$M$ (g)
1	8
2	16
3	24
4	32

Sea $M$ una magnitud física cualquiera y $V$ otra, indicaremos que existe una proporcionalidad directa por el símbolo $\alpha$ (que se lee "proporcional a"), esto es:

$$M \ \alpha \ V$$

Si dos magnitudes son proporcionales se cumple que:

$$\frac{M}{V}=k,\quad \text{con $k$ constante.}$$

Donde $k$ se denomina constante de proporcionalidad. Por lo tanto, la expresión $\frac{M}{V}=k$ se puede escribir como:

$$M = kV$$

Proporcionalidad inversa

Dos magnitudes son inversamente proporcionales si al aumentar una de ellas $N$ veces, entonces la otra magnitud disminuye $N$ veces.

Dos cantidades $M$ y $V$ son inversamente proporcionales si su producto es constante, esto es:

$$M \cdot V = k,\quad \text{con $k$ constante.}$$

Representación gráfica de una relación de proporcionalidad directa

Es posible analizar la dependencia entre dos magnitudes a través del método gráfico. Tomando en cuenta nuevamente el caso de los bloques de hierro, esbozaremos la gráfica de la masa $M$ versus el volumen $V$.

• Se trazan dos rectas perpendiculares.
• Sobre la recta horizontal, que llamaremos abscisa, se sitúan los valores de la variable independiente, que en este caso es el volumen. En la recta vertical, que llamaremos ordenada, se sitúan los valores de la variable dependiente, en este caso la masa.
• Se ubican los puntos en la gráfica. Teniendo todos los puntos, se debe trazar la mejor curva que se ajuste a los datos.

Es posible comprobar que, en este caso, la gráfica es una recta que pasa por el origen, lo que sucede siempre que tenemos una proporcionalidad directa.

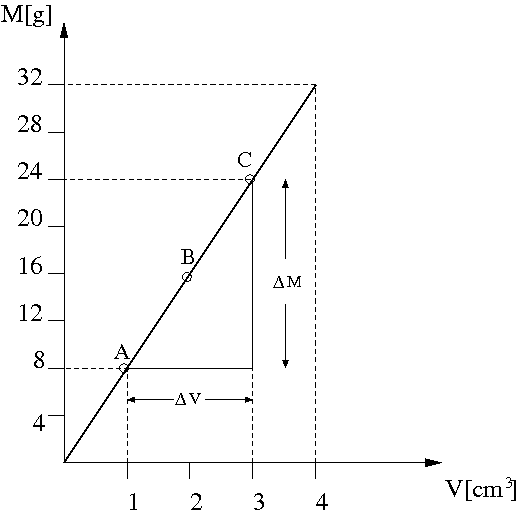
Pendiente de una recta

Tomemos dos pares de datos cualquiera de la relación $M$ versus $V$, por ejemplo los puntos $A$ y $C$.

En el punto $A$ el volumen es $V_A = 1$ cm$^3$ y la masa es $M_A = 8$ g. Por otro lado, en el punto $C$, $V_C = 3$ cm$^3$ y $M_C = 24$ g.

Nota que existe una variación tanto de la masa como del volumen al pasar del punto $A$ al $C$. Denotamos la variación de una magnitud con la letra griega delta $\Delta$:

• $\Delta V = V_C - V_A$
• $\Delta M = M_C - M_A$

Se define la pendiente $m$ de una recta como:

$$m = \frac{\Delta M}{\Delta V}$$

Mientras mayor sea la pendiente, mayor será el ángulo que forma la recta con la horizontal. También se interpreta como una mayor rapidez en la variación de una magnitud respecto de otra.

En este ejemplo, la pendiente es $m = 8$ g/cm$^3$, coincidiendo con el valor de la constante de proporcionalidad. Esto siempre sucede cuando entre las magnitudes existe una proporcionalidad directa.

En Matemática, la representación gráfica de una relación de proporcionalidad directa es la de una función lineal, correspondiente a una recta que pasa por el punto $(0, 0)$.

Si los puntos $(x_1, y_1)$ y $(x_2, y_2)$ pertenecen a la gráfica de una función lineal, la pendiente $m$ se calcula como:

$$m = \dfrac{y_2 - y_1}{x_2 - x_1}$$