Ecuaciones de Primer Grado y Sistemas de Ecuaciones - PAES M1

Este resumen corresponde al Eje Temático Álgebra y funciones en las unidades temáticas Ecuaciones lineales de primer grado y Sistemas de ecuaciones lineales, las que se describen como:

• Resolución de ecuaciones lineales.
• Problemas que involucren ecuaciones lineales en diversos contextos.
• Resolución de sistemas de ecuaciones lineales.
• Casos en los cuales un sistema tiene una única solución, infinitas soluciones o no tiene solución.
• Problemas que involucren sistemas de ecuaciones lineales en diversos contextos.

¿Qué es una ecuación?

Una ecuación es la representación de la igualdad entre dos expresiones algebraicas.

Una ecuación posee al menos una incógnita o término desconocido, que habitualmente se representa con la letra x.

Ecuación de primer grado con una incógnita

Cuando una ecuación posee una incógnita y ésta tiene como mayor exponente el número 1, se denomina ecuación lineal o ecuación de primer grado con una incógnita.

Una ecuación lineal con una incógnita (x) se puede escribir en la forma:

$$ax = b,$$

donde a y b son números racionales y $a \neq 0$.

Resolver una ecuación de primer grado con una incógnita significa determinar el valor que debe tomar la incógnita para que la igualdad sea verdadera.

Enunciado: Una ecuación conserva la igualdad cuando se suma, resta, multiplica o divide una misma cantidad a ambos lados de la igualdad.

Ecuación de primer grado con dos incógnitas

Cuando una ecuación posee dos incógnitas y éstas tienen como mayor exponente el número 1, se denomina ecuación lineal o ecuación de primer grado con dos incógnitas.

Una ecuación lineal con dos incógnitas (x e y) se puede escribir en la forma:

$$ax + by = c,$$

donde a, b y c son números racionales, $a \neq 0$ y $b \neq 0$.

Una ecuación lineal de dos incógnitas posee infinitas soluciones; es decir, existen infinitas combinaciones de pares ordenados $(x, y)$ que satisfacen la igualdad.

Enunciado: Estas ecuaciones se pueden escribir como $y = -\dfrac{a}{b}x + \dfrac{c}{b}$, cuya gráfica corresponde a una recta con pendiente $-\frac{a}{b}$ y ordenada al origen en $\bigl(0, \frac{c}{b}\bigr)$.

Sistemas de ecuaciones lineales con dos incógnitas

Un sistema de ecuaciones es un conjunto de ecuaciones con las mismas incógnitas.

Un sistema de ecuaciones lineales es aquel en el que cada ecuación es lineal. Dos ecuaciones lineales con las mismas incógnitas forman un sistema de ecuaciones lineales con dos incógnitas.

Un sistema de ecuaciones lineales con dos incógnitas x e y tiene la forma:

$$\begin{cases} ax + by = c \\ dx + ey = f \end{cases}$$

donde a, b, c, d, e y f son números racionales.

Una solución del sistema es un par ordenado $(x, y)$ que, al sustituirlo en ambas ecuaciones, satisface las igualdades.

Enunciado: Para un sistema de ecuaciones lineales con dos incógnitas, se cumple una de las siguientes afirmaciones:

1. El sistema tiene exactamente una solución.
2. El sistema no tiene solución.
3. El sistema tiene un número infinito de soluciones.

Sistema de ecuaciones lineales con una única solución

Considera el sistema:

$$\begin{cases} ax + by = c \\ dx + ey = f \end{cases}$$

con a, b, c, d, e y f diferentes de cero. Gráficamente, las rectas correspondientes a cada ecuación son secantes y su punto de intersección es la solución única.

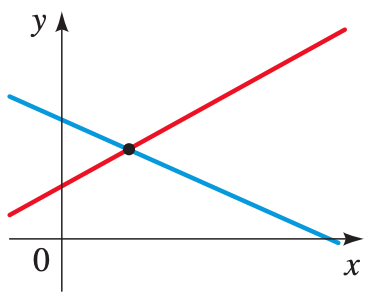
Enunciado: Algebraicamente se cumple que:

$$\frac{a}{d} \neq \frac{b}{e}$$

Sistema de ecuaciones lineales con infinitas soluciones

Considera el mismo sistema anterior. Cuando las rectas correspondientes son coincidentes, el sistema tiene infinitas soluciones.

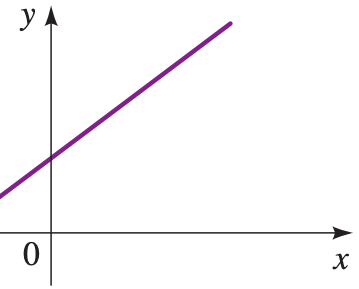
Enunciado: Algebraicamente se cumple que:

$$\frac{a}{d} = \frac{b}{e} = \frac{c}{f}$$

Sistema de ecuaciones lineales sin solución

Cuando las rectas correspondientes son paralelas y no se intersectan, el sistema no tiene solución.

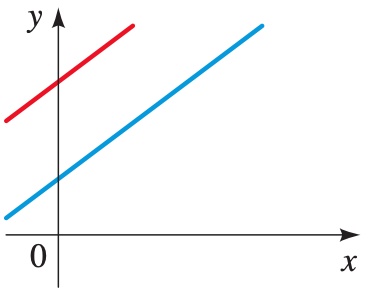
Enunciado: Algebraicamente se cumple que:

$$\frac{a}{d} = \frac{b}{e} \neq \frac{c}{f}$$

Métodos algebraicos de resolución de sistemas de ecuaciones lineales con dos incógnitas

Para resolver un sistema de ecuaciones lineales con dos incógnitas se utilizan tres métodos: igualación, sustitución y reducción.

Método de igualación

Para usar el método de igualación:

1. Despeja la misma incógnita en ambas ecuaciones.
2. Igualar las expresiones obtenidas y resolver para la incógnita restante.
3. Sustituir el valor encontrado en una de las ecuaciones originales y resolver para la otra incógnita.

Método de sustitución

Para usar el método de sustitución:

1. Despejar una incógnita en una de las ecuaciones.
2. Sustituir esa expresión en la otra ecuación y resolver.
3. Sustituir el valor obtenido en una de las ecuaciones originales para hallar la segunda incógnita.

Método de reducción

Para usar el método de reducción:

1. Multiplicar una o ambas ecuaciones por números que permitan cancelar una incógnita (coeficientes opuestos o iguales).
2. Sumar o restar las ecuaciones resultando en una sola ecuación con una incógnita.
3. Resolver la ecuación obtenida.
4. Sustituir el valor hallado en una de las ecuaciones originales para hallar la segunda incógnita.