Función Cuadrática - PAES M1

Detrás del movimiento que describe un proyectil, la distancia que recorre un objeto que acelera o en la caída libre de una manzana, está presente la función cuadrática. El concepto de función es transversal a todas las ciencias tanto naturales como sociales, por tal motivo es importante poder interpretar sus gráficas y desde ahí extraer conclusiones.

Se denomina función cuadrática $f$ a aquella definida como:

$$\begin{array}{ccl} f: \mathbb{R} &\longrightarrow& \mathbb{R} \\ x &\longmapsto& f(x) = ax^2 + bx + c \end{array}$$

donde $a$, $b$ y $c$ son constantes reales con $a\neq 0$. Existe una relación directa entre la función cuadrática y una ecuación de segundo grado del tipo $y = ax^2 + bx + c$ que iremos desarrollando en esta guía.

Características

La función cuadrática no es inyectiva de $\mathbb{R}$ a $\mathbb{R}$, ya que existen imágenes que tienen asociadas dos pre-imágenes. Veamos un caso puntual para $f(x) = x^2$:

$$\begin{aligned} f(3) &= 3^2 = 9 \\ f(-3) &= (-3)^2 = 9 \end{aligned}$$

En general, para cualquier $x \in \mathbb{R}$ se cumplirá que $x^2 = (-x)^2$, por lo tanto, existen imágenes que tienen asociadas dos pre-imágenes.

La función cuadrática tampoco es sobreyectiva de $\mathbb{R}$ a $\mathbb{R}$ porque el recorrido no es igual al codominio. En estas condiciones, la función inversa solo existirá si "arreglamos" el dominio y el codominio de la función. Para ver estas características con más claridad es recomendable graficar la función.

Función cuadrática

Sean $a,b,c \in \mathbb{R}$ y $a \neq 0$. Llamaremos función cuadrática a aquella de la forma:

$$f(x) = ax^2 + bx + c$$

La representación gráfica de una función cuadrática se llama parábola.

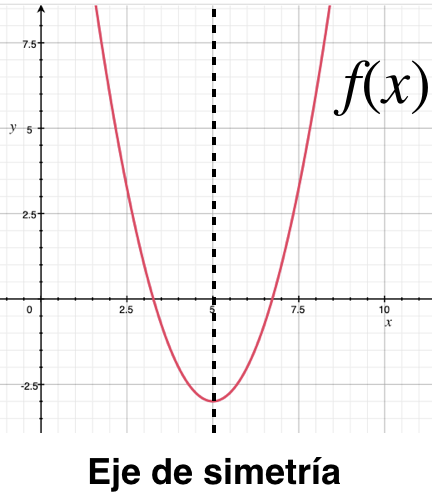
Esta curva tiene un eje de simetría paralelo al eje de las ordenadas.

Dominio y Recorrido

El dominio de la función cuadrática es $\mathbb{R}$.

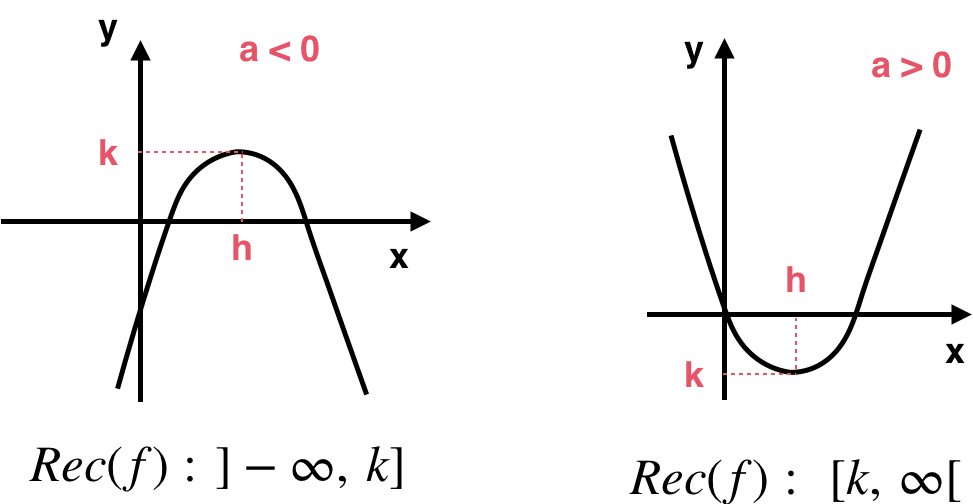
El recorrido depende del signo del coeficiente $a$ de la función $f(x) = ax^2 + bx + c$.

Concavidad

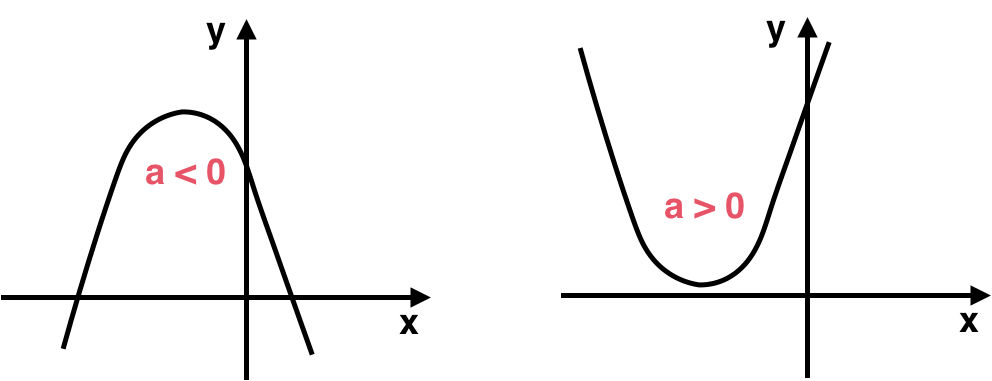
Es la apertura que tiene la parábola y depende directamente del valor de $a$.

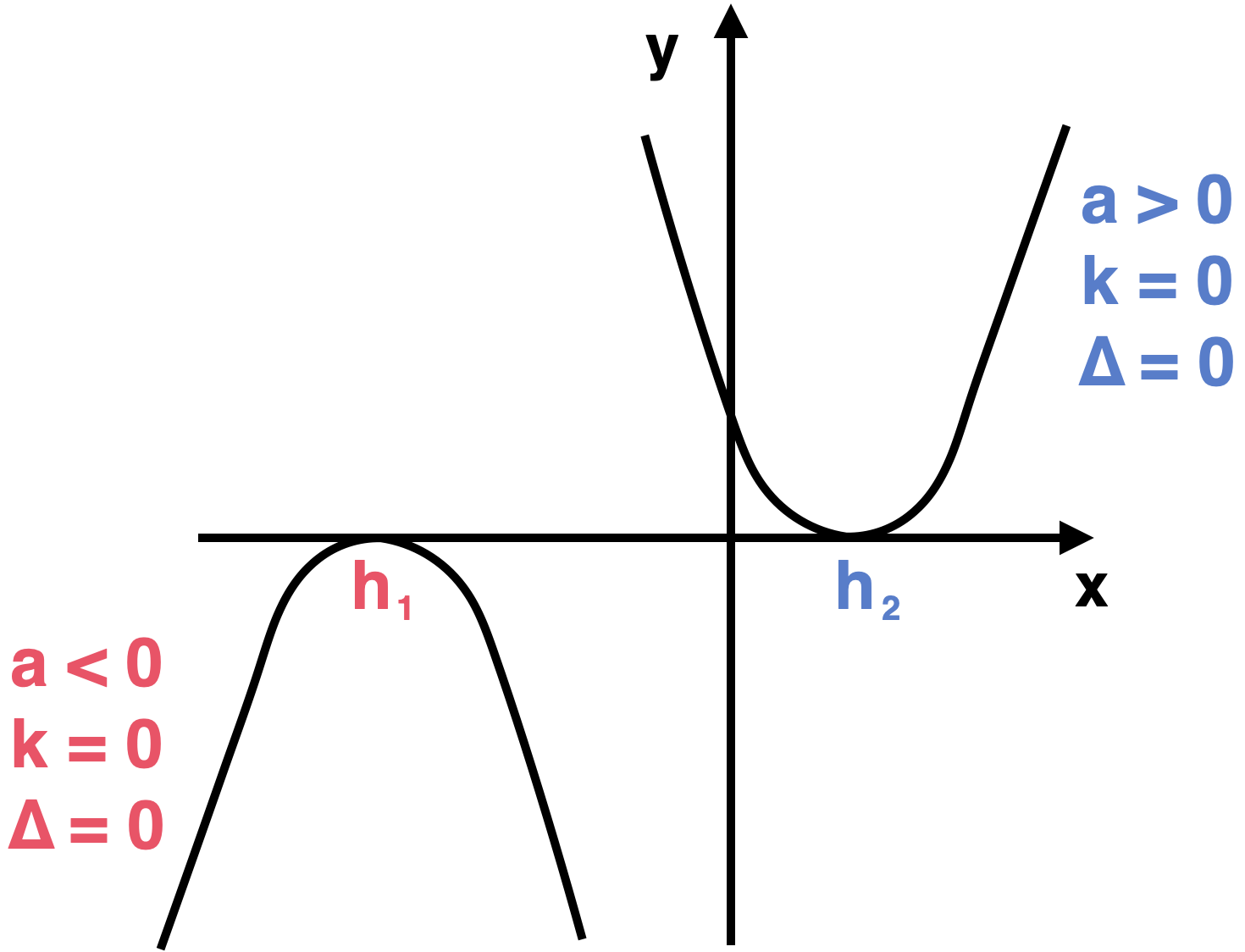
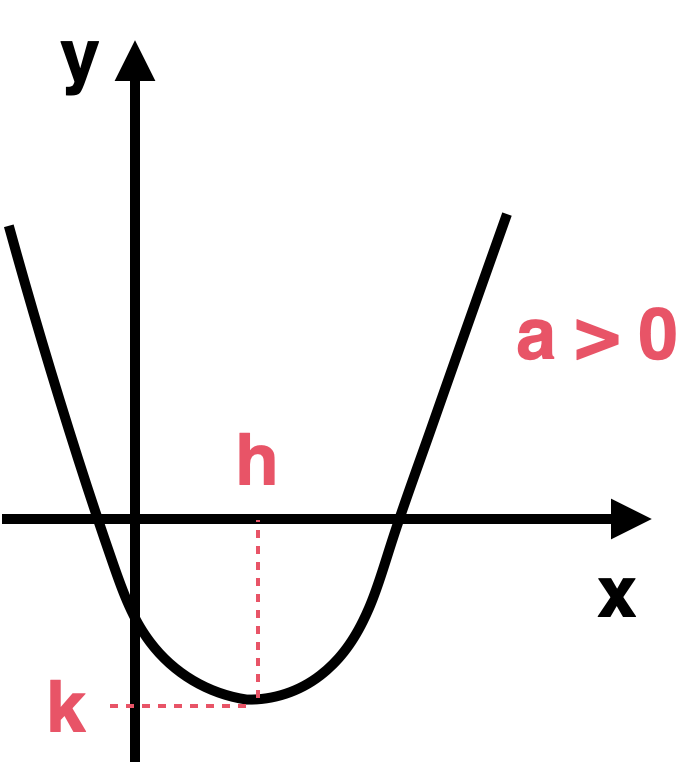
• Si $a > 0$, las "ramas" de la parábola van hacia arriba (la parábola está "contenta c:").
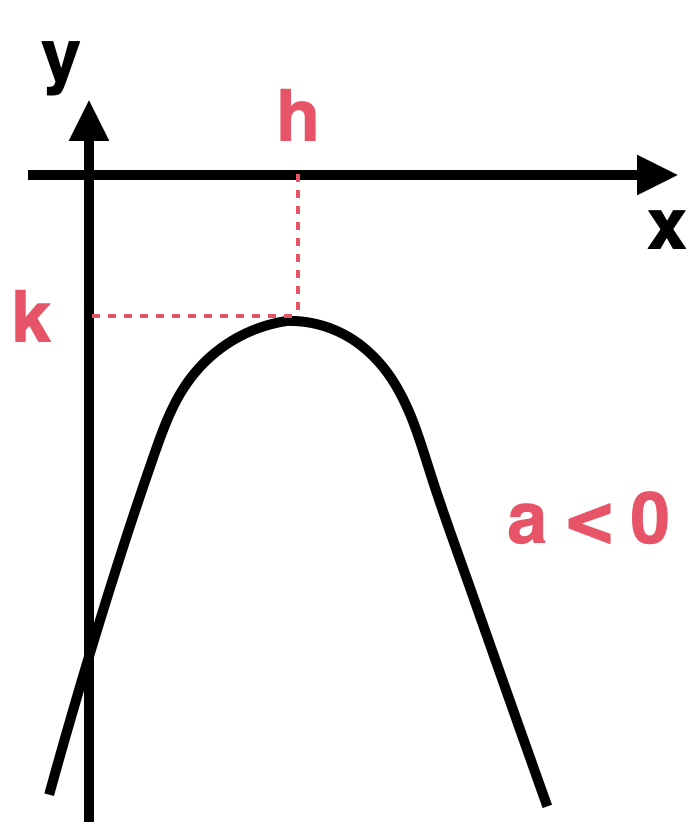
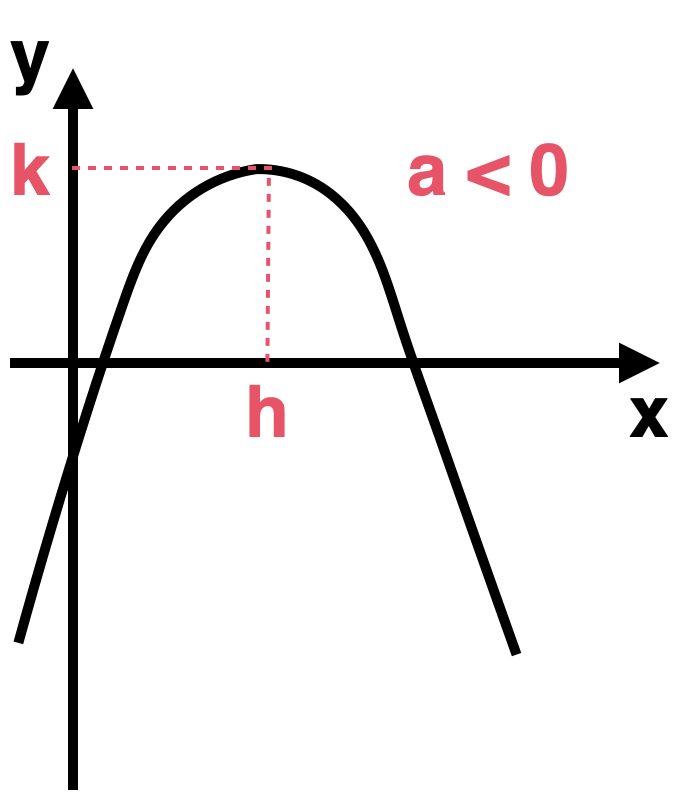
• Si $a < 0$, las "ramas" de la parábola van hacia abajo (la parábola está "triste :c").

Intersección con el eje de las ordenadas

La intersección con el eje de las ordenadas (eje $y$) se da cuando $x = 0$, de modo que $y = f(0) = c$. Así, el punto de intersección es $(0, c)$.

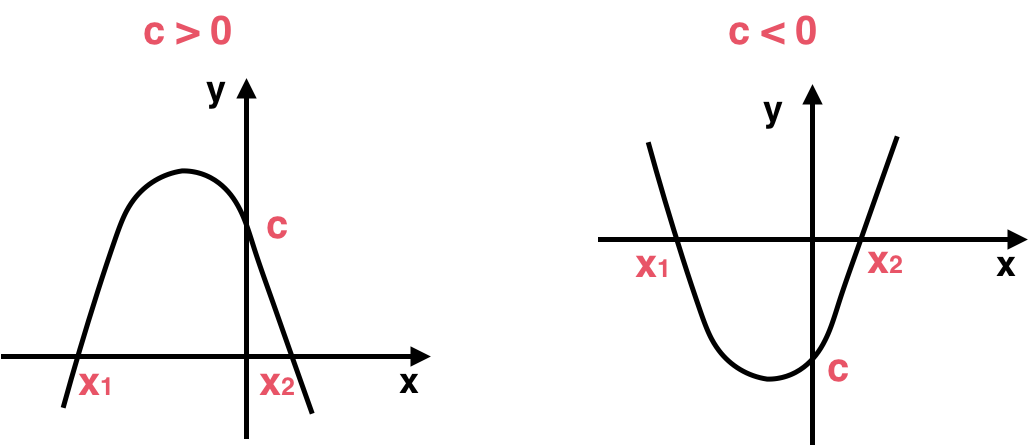
Intersección con el eje de las abscisas

La intersección con el eje de las abscisas (eje $x$) se da cuando $y = 0$, resolviendo:

$$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$$

Según el discriminante $\Delta = b^2 - 4ac$:

• Si $\Delta = 0$, la parábola intersecta en un solo punto (coordenada de su vértice).
• Si $\Delta > 0$, intersecta en dos puntos diferentes.
• Si $\Delta < 0$, no intersecta en puntos reales.

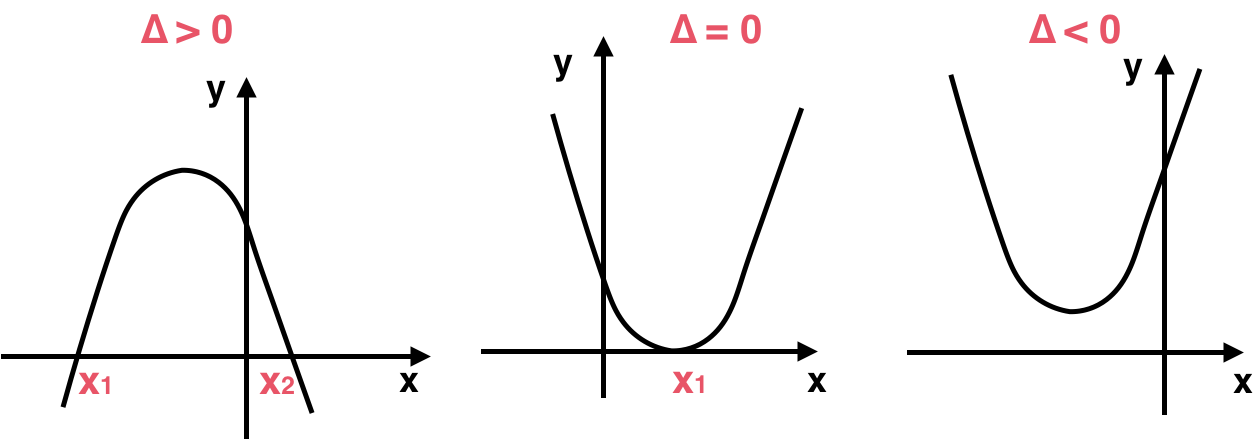
Vértice y eje de simetría

La función cuadrática $f(x)=ax^2+bx+c$ tiene un valor mínimo si $a \gt 0$ y un máximo si $a \lt 0$. Este valor corresponde a la coordenada $y$ del vértice:

$$\text{vértice} = \left(-\frac{b}{2a}, -\frac{\Delta}{4a}\right)$$

El eje de simetría se da en:

$$x = -\frac{b}{2a}$$

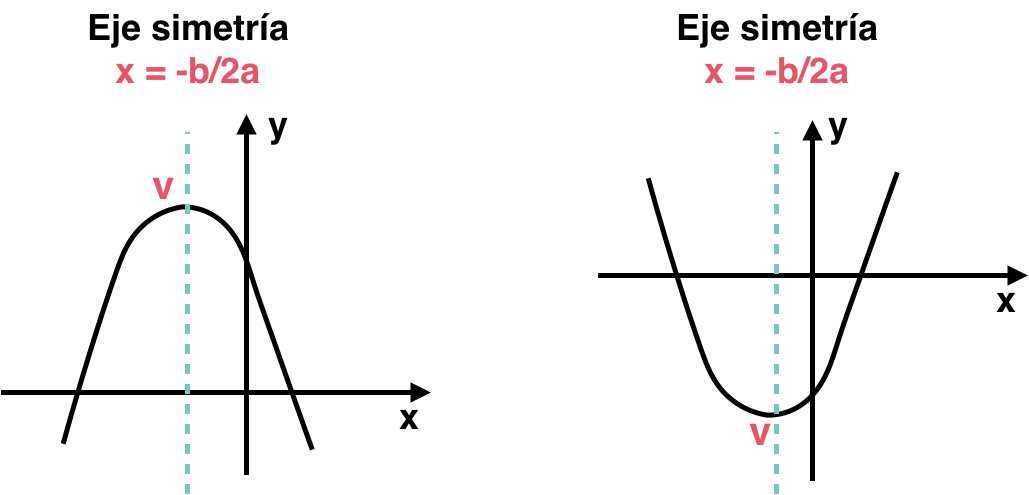
Completación de cuadrados

Es una técnica para factorizar en donde reescribimos una expresión algebraica para que quede de la forma:

$$(x-h)^2 + k$$

Ejemplo: Reescribir la igualdad $x^2 + 6x + 5 = 0$ para $x \in \mathbb{R}$.

$$\begin{aligned} x^2 + 6x + 5 &= 0 \\ x^2 + 2(x \cdot 3) + 5 &= 0 \\ x^2 + 2(x \cdot 3) + 5 + 9 &= 9 \\ x^2 + 2(x \cdot 3) + 9 + 5 &= 9 \\ (x+3)^2 + 5 &= 9 \\ (x+3)^2 &= 4 \end{aligned}$$

Con esto logramos reescribir la igualdad $x^2 + 6x + 5 = 0$ como $(x+3)^2 = 4$, lo cual es muy conveniente para identificar el vértice de la parábola por inspección.

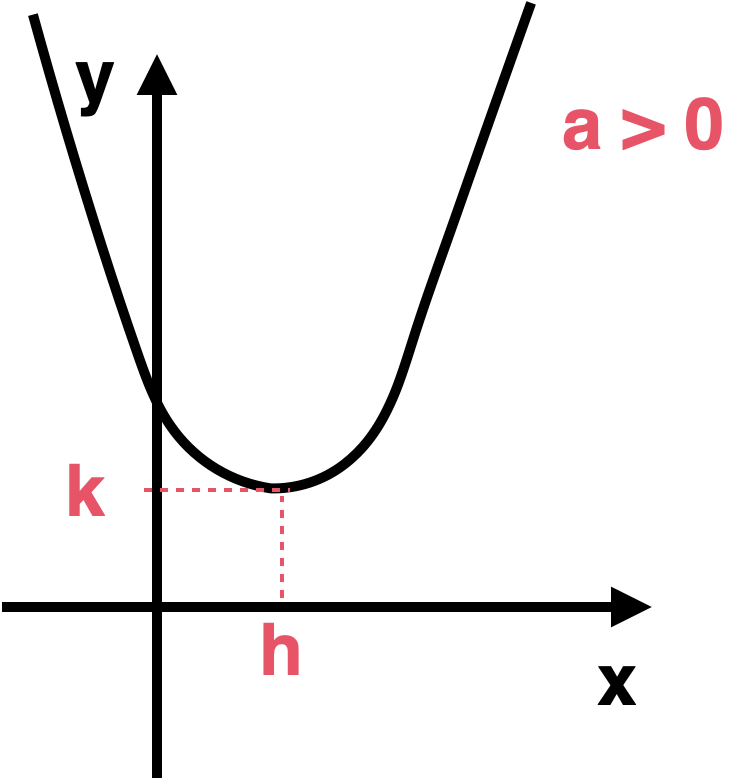
Forma estándar de la función cuadrática

La función cuadrática también puede expresarse en su forma estándar

$$f(x) = a(x - h)^2 + k$$

La ventaja de esta forma es visualizar rápidamente su vértice y traslaciones.

Enunciado: El vértice de la forma estándar $f(x) = a(x - h)^2 + k$ es $(h,k)$, y el eje de simetría es $x = h$.

Relación entre la forma general y la forma estándar

La relación entre los coeficientes de $f(x) = ax^2 + bx + c$ y $f(x) = a(x - h)^2 + k$ es:

$$\begin{aligned} a &= a \\ h &= -\frac{b}{2a} \\ k &= c - \frac{b^2}{4a} \end{aligned}$$

Traslación de la función cuadrática

La función $f(x) = a(x - h)^2 + k$ se desplaza $h$ unidades en el eje $x$ y $k$ unidades en el eje $y$, con respecto al origen.

Intersección con los ejes cartesianos

Sea $f(x) = a(x - h)^2 + k$ con $a \neq 0$.

• Caso 1: $a>0$, $k>0$. No intersecta el eje $x$ (discriminante negativo), intersecta el eje $y$ en valores positivos.

• Caso 2: $a \gt 0$, $k \lt 0$. Intersecta eje $x$ en dos puntos (discriminante positivo), eje $y$ en valores positivos o negativos.

• Caso 3: $a \lt 0$, $k \lt 0$. No intersecta eje $x$ (negativo), intersecta eje $y$ en valores negativos.

• Caso 4: $a \lt 0$, $k \gt 0$. Intersecta eje $x$ en dos puntos (positivo), eje $y$ en valores positivos o negativos.

• Caso 5: $k=0$. Intersecta eje $x$ en un punto (discriminante 0), eje $y$ según signo de $a$.