¿Qué es un vector?

Un vector es un segmento de recta dirigido que se caracteriza por tener magnitud o módulo, dirección y sentido. En el plano cartesiano, los vectores se representan gráficamente con una flecha. La magnitud de un vector $\overrightarrow{AB}$ es su longitud, es decir, la distancia entre el inicio $A$ (cola) y el final $B$ (punta de flecha) y se denota de la forma $|\overrightarrow{AB}\,|$.

El sentido del vector está dado por la punta de la flecha que lo representa e indica hacia donde se dirige. La dirección del vector es la orientación o el ángulo que forma la recta que contiene al vector con el eje horizontal del plano cartesiano.

Para representar un vector en el plano cartesiano se deben conocer sus componentes, es decir, las coordenadas $x$ e $y$ que definen al vector $(x, y)$. Para el vector $\overrightarrow{AB}$, sus puntos extremos son $A$ y $B$. Si el punto $A$ tiene coordenadas $(x_1, y_1)$ y el punto $B$ tiene coordenadas $(x_2,y_2)$, las componentes del vector $\overrightarrow{AB}$ están dadas por la diferencia de las abscisas de los puntos final e inicial y la diferencia de las ordenadas de los mismos:

$\overrightarrow{AB}=(x_2,y_2)-(x_1,y_1)=(x_2 - x_1, y_2-y_1)$

Veamos un ejemplo para comprender la definición anterior: Observa el vector $\overrightarrow{AB}$ en el plano cartesiano:

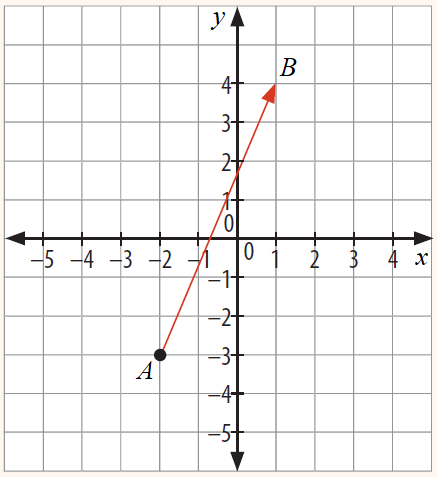
Las coordenadas del punto $A$ son $(-2,-3)$ y las coordenadas del punto $B$ son $(1,4)$, entonces las componentes o coordenadas del vector $\overrightarrow{AB}$ están dadas por:

$\overrightarrow{AB}=(1,4)-(-2,-3)=(1--2,4--3)=(1+2,4+3)=(3,7)$

Se concluye que $\overrightarrow{AB}=(3,7)$.

Gráficamente puedes verificar que el vector $\overrightarrow{AB}$ representado en el plano cartesiano posee $3$ unidades en la abscisa o eje $x$ y $7$ unidades en la ordenada o eje $y$:

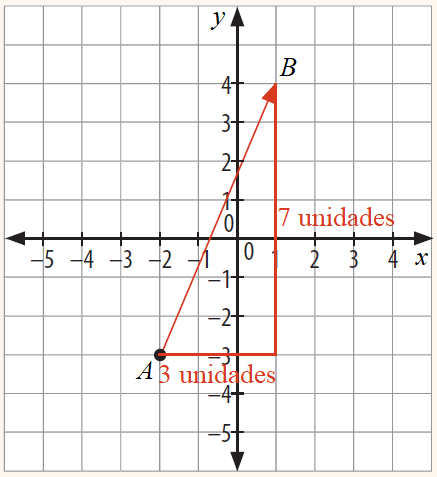
Observa el vector $(4,3)$ representado en el plano cartesiano:

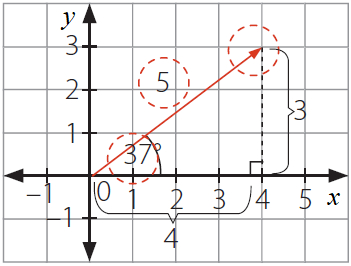
El vector $(4,3)$ tiene sentido noroeste dado por la punta de la flecha, su dirección es 37º con respecto al eje $x$ dado por el ángulo que forma con este y su magnitud es $5$ unidades, es decir, la longitud de la flecha es $5$. ¿Cómo determinamos la magnitud del vector $(4,3)$?

La magnitud o módulo, dado que corresponde a una distancia, siempre será un número positivo y puede ser calculada con el teorema de Pitágoras. En este caso, los catetos del triángulo rectángulo que se forma con las proyecciones de los ejes del plano cartesiano y el vector son $4$ y $3$ unidades como puedes observar en la imagen, mientras que la magnitud o módulo del vector corresponde a la hipotenusa $h$ del triángulo:

$h^2=4^2+3^2$ $h^2=16+9$ $h^2=25$ $h=\sqrt{25}$ $h=5$

Por lo tanto, la magnitud o módulo del vector $(4,3)$ es igual a $5$.

En términos generales, si un vector $\vec v\,$ tiene componentes $(v_x, v_y)$, su magnitud $|\vec v|$ está dada por:

$|\vec v\,|=\sqrt{v_x^2+v_y^2\;}$

Cuando dos vectores poseen igual magnitud, sentido y dirección, se dice que estos vectores son equivalentes.

Multiplicación de un vector por un escalar

Se denomina escalar a cualquier cantidad perteneciente al conjunto de los números reales que carece de dirección y sentido.

Para multiplicar un vector $(x, y)$ por un escalar $k$ se debe multiplicar la componente $x$ y la componente $y$ del vector por el escalar $k$:

$k\cdot (x,y)=(k\cdot x,k\cdot y)$

Ejemplo: Sea $\vec{v}= (2,7)$ un vector y $10$ un escalar. ¿Cuál es el resultado de $10\cdot \vec v$?

$10\cdot \vec{v} = 10\cdot (2,7)=(10\cdot 2, 10\cdot 7)=(20,70)$

Es decir, $10\cdot \vec v=(20,70)$.

La multiplicación de un vector por un escalar también es denominada ponderación de un vector por un escalar.

Gráficamente, si $k>0$ el resultado corresponde a un vector con la misma dirección y sentido que el vector $(x,y)$, pero con una longitud igual a $k$ veces su longitud. Por otro lado, si $k<0$ el resultado corresponde a un vector con la misma dirección y sentido opuesto al vector $(x,y)$, pero con una longitud igual a $k$ veces su longitud.

Adición y sustracción de vectores

Sean $\vec{v}=(x_1,y_1)$ y $\vec{w}=(x_2,y_2)$ vectores en el plano cartesiano. Definimos las operaciones adición ($+$) y sustracción ($-$) como:

$\vec{v}+\vec{w}=(x_1,y_1)+(x_2,y_2)=(x_1+x_2,y_1+y_2)$

$\vec{v}-\vec{w}=(x_1,y_1)-(x_2,y_2)=(x_1-x_2,y_1-y_2)$

Nota que en ambas operaciones el resultado también corresponde a un vector del plano cartesiano.

Gráficamente, el vector resultante de la adición $\vec{v}+\vec{w}$ corresponde a la diagonal del paralelogramo formado a partir de los vectores $\vec{v}$ y $\vec{w}$. Veamos un ejemplo para comprender esta afirmación:

Observa los vectores $\vec{v}=(2,2)$ y $\vec{w}=(-3,2)$ representados en el plano cartesiano:

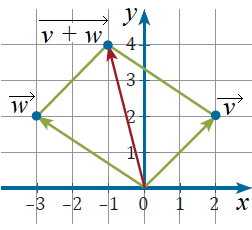
Puedes verificar que el resultado de la adición de $\vec{v}$ y $\vec{w}$ es el vector $\overrightarrow{v+w}$ representado en el plano cartesiano anterior:

$\vec{v}+\vec{w}=(2,2)+(-3,2)=(2+-3,2+2)=(-1,4)$

Como puedes observar, el vector $\overrightarrow{v+w}$ corresponde a la diagonal del paralelogramo formado a partir de los vectores $\vec{v}$ y $\vec{w}$.

Nota que restar el vector $(x,y)$ es equivalente a sumar el vector $(-x,-y)$, por lo que la interpretación geométrica es idéntica a la dada para la adición de vectores.

Ejemplo 1: Sean $\vec{z}=(3,2)$ y $\vec{w}=(-5,8)$ vectores, ¿cuál es el resultado de $\vec{z}+\vec{w}$?

$$\begin{aligned} \vec{z}+\vec{w} &= (3,2)+(-5,8) \\ &= (3 + (-5),\; 2 + 8) \\ &= (-2,\; 10) \end{aligned}$$

Ejemplo 2: Sean $\vec p=(-6,-1)$ y $\vec q=(-2,4)$ vectores, ¿cuál es el resultado de $\vec{p}+\vec{q}$ ?

$$\begin{aligned} \vec{p}+\vec{q} &=(-6,-1)+(-2,4) \\ &=(-6+-2,-1+4) \\ &=(-8,3) \end{aligned}$$

Ejemplo 3: Sean $\vec{z}=(3,2)$ y $\vec{w}=(-5,8)$ vectores, ¿cuál es el resultado de $\vec{z}-\vec{w}$?

$$\begin{aligned} \vec{z}-\vec{w} &=(3,2)-(-5,8) \\ &=(3--5,2-8)\\ &=(3+5,2-8)\\ &=(8,-6) \end{aligned}$$

Ejemplo 4: Sean $\vec p=(-6,-1)$ y $\vec q=(-2,4)$ vectores, ¿cuál es el resultado de $\vec{p}-\vec{q}$ ?

$$\begin{aligned} \vec{p}-\vec{q} &=(-6,-1)-(-2,4)\\ &=(-6--2,-1-4)\\ &=(-6+2,-1-4)\\ &=(-4,-5) \end{aligned}$$

Traslaciones de figuras geométricas usando vectores

La traslación es una transformación isométrica que corresponde al movimiento de una figura en una dirección, en un sentido y en una magnitud dada. La dirección, sentido y magnitud del desplazamiento de la figura pueden ser representados por un vector de traslación.

Sea $P$ un punto del plano cartesiano que posee coordenadas $(x,y)$. Si al punto $P$ se le debe aplicar una traslación según el vector $\vec{t}=(t_x, t_y)$, la imagen o punto que se obtiene luego de trasladar el punto $P$ según el vector $\vec t$ posee las coordenadas $(x+t_x, y+t_y)$. Es decir, para trasladar un punto del plano cartesiano usando cierto vector traslación, el punto debe tratarse como vector y se debe resolver la operación $(x,y)+(t_x,t_y)$.

Nota que en este caso el vector obtenido corresponde en realidad a un punto del plano cartesiano.

Ejemplo: Al punto $(6,-4)$ se le aplicó una traslación y se obtuvo el punto $(12,-8)$. Al aplicar al punto $(-3,5)$ la misma traslación, ¿qué punto se obtiene?

Al punto $(6,-4)$ se le aplicó una traslación usando un vector traslación desconocido $(t_x,t_y)$ y se obtuvo el punto $(12,-8)$. Por lo tanto, se debe cumplir que:

$(6,-4)+(t_x,t_y)=(12,-8)$

Es decir:

$6+t_x=12 \; \Rightarrow\; t_x=12-6 \;\Rightarrow\; t_x=6$

$-4+t_y=-8 \; \Rightarrow\; t_y=-8+4=-4$

Por lo tanto, concluimos que el vector traslación desconocido originalmente es $(6,-4)$. Para conocer cuál es el punto obtenido al aplicar al punto $(-3,5)$ la traslación según el vector $(6,-4)$ se debe resolver $(-3,5)+(6,-4)$:

$(-3,5)+(6,-4)=(-3+6,5+-4)=(3,1)$

Concluimos que el punto obtenido al aplicar al punto $(-3,5)$ la traslación según el vector $(6,-4)$ posee coordenadas $(3,1)$.