Área de figuras planas
Este resumen corresponde al Eje Temático Geometría en la unidad temática Área de figuras planas, la que se describe como:
- Área de triángulos, paralelogramos, trapecios y círculos.
- Problemas que involucren área de triángulos, paralelogramos, trapecios y círculos en diversos contextos.
Área de figuras planas
El área de una figura plana corresponde a la medida de la región o superficie encerrada por los límites de la figura.
Área de triángulos
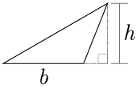
En términos generales, el área de un triángulo corresponde al semiproducto entre una de sus bases y la altura correspondiente del mismo. Una altura es la recta perpendicular trazada desde un vértice al lado opuesto (o su prolongación).
Triángulo equilátero
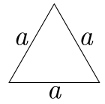
El área de un triángulo equilátero de lado es . Recuerda que la altura de un triángulo equilátero de lado es .
Triángulo rectángulo
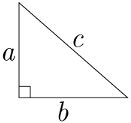
El área de un triángulo rectángulo se puede obtener alternativamente como el semiproducto de sus catetos. Cuando se desconoce el valor de uno de sus lados, este puede ser expresado en función de los lados restantes al ocupar el Teorema de Pitágoras.
Área de paralelogramos
Un paralelogramo es un polígono con cuatro lados cuyos lados opuestos son paralelos, es decir, un paralelogramo es un cuadrilátero con ambos pares de lados opuestos paralelos. Las figuras planas que se clasifican como paralelogramos son el cuadrado, el rectángulo, el rombo y el romboide.
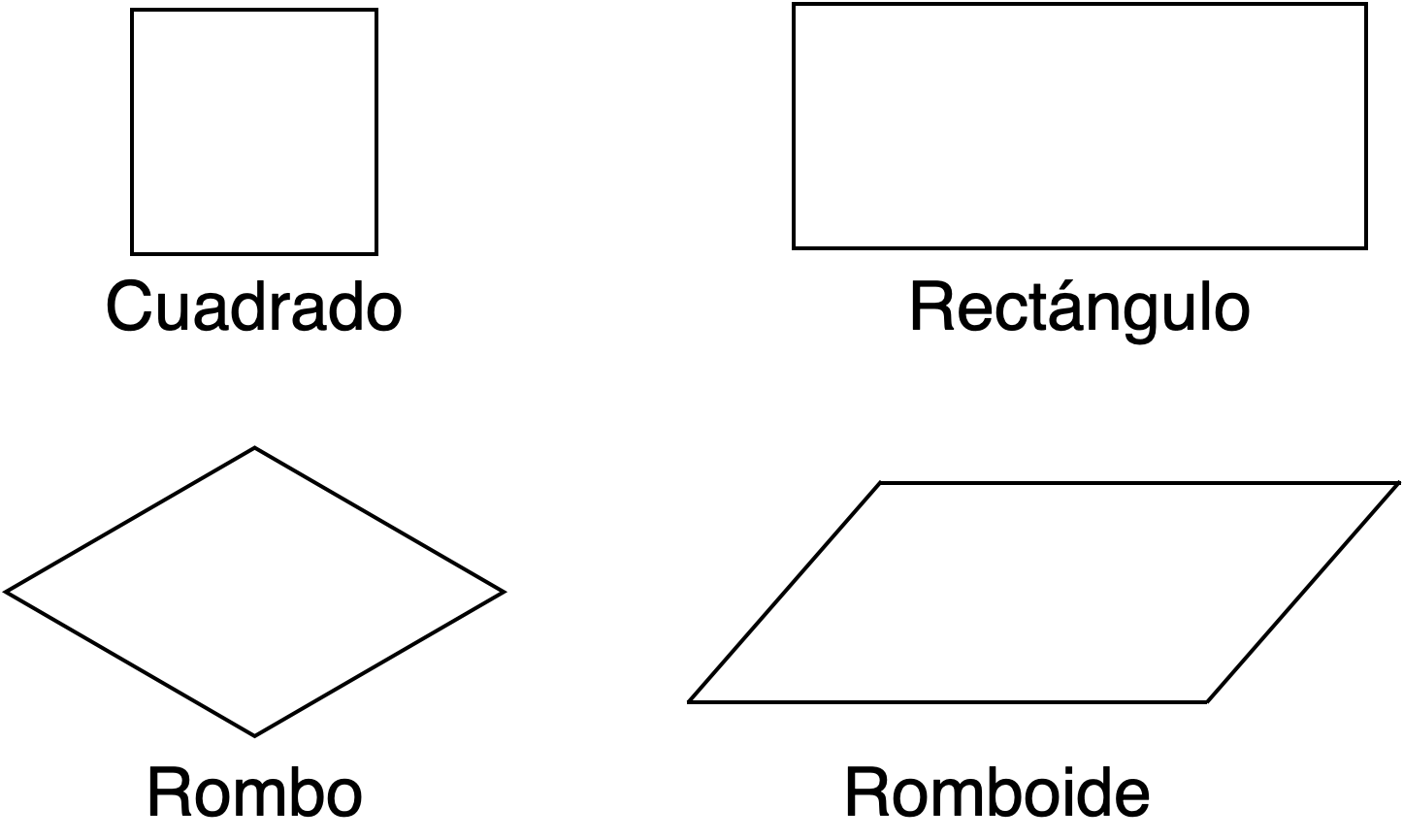
- El cuadrado es un paralelogramo con cuatro lados congruentes y cuatro ángulos interiores rectos.
- El rombo es un paralelogramo con cuatro lados congruentes y dos pares de ángulos interiores congruentes.
- El rectángulo es un paralelogramo con dos pares de lados congruentes y cuatro ángulos interiores rectos.
- El romboide es un paralelogramo con dos pares de lados congruentes y dos pares de ángulos interiores congruentes.
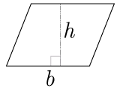
En términos generales, el área de un paralelogramo corresponde al producto entre su base y su altura .
El área de un cuadrado de lado es .
El área de un rectángulo de lado menor y lado mayor es .
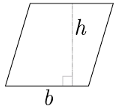
El área de un romboide se puede calcular como el producto entre su base y su altura.
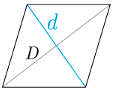
El área de un rombo se puede calcular como el semiproducto de sus diagonales o también como el producto entre su base y su altura.
Las diagonales del rombo se dimidian perpendicularmente, por lo que puede descomponerse en 4 triángulos rectángulos.
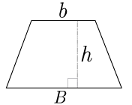
Área de trapecios
Un trapecio es un cuadrilátero que tiene dos de sus lados paralelos, llamados base mayor y base menor .
El área de un trapecio es el semiproducto entre la suma de sus bases y su altura .
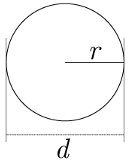
Área de círculos
El área de un círculo de radio es . El área de un círculo expresado en función de su diámetro es .