PAES - Introducción a los Números Racionales

Información PAES

Este resumen corresponde al Eje Temático Números en la unidad temática Conjunto de los números racionales la que se describe como:

• Operaciones y orden en el conjunto de los números racionales.
• Problemas que involucren el conjunto de los números racionales en diversos contextos.

Números Racionales

La idea de fracción se originó de la necesidad social de medir con mayor exactitud algunas magnitudes, puesto que los números naturales resultaron ser insuficientes para este fin. Los primeros registros que existen sobre números fraccionarios son del año 1650 a.C. en papiros egipcios, en donde se usaban fracciones para representar partes de una unidad. Los números fraccionarios, considerados como razones entre números naturales, se presentan en el libro VII de Elementos de Euclides, alrededor del 300 a.C.

En el siglo XIII, Leonardo de Pisa o “Fibonacci” introdujo el sistema de numeración decimal en Europa, desarrollado por indios y árabes previamente. En este sistema emergen las fracciones decimales, siendo Leonardo de Pisa el autor del concepto de número quebrado o número “ruptu”, usando la raya fraccionaria que actualmente se emplea para separar numerador y denominador.

En el siglo XIX, la comunidad matemática de la época manifiesta un cambio de actitud hacia lo que se consideraba imposible: la existencia de un conjunto infinito de símbolos que representan números, que incluye a los números naturales y que cumple ciertas propiedades de orden y operatoria. En 1822, Martin Ohm da una primera propuesta de definición de número racional, pero alrededor de 1860 Karl Weierstrass los define como:

$\left\lbrace p\cdot q^{-1} \; / \;\; p, q \in \mathbb{Z}, q \neq 0 \right\rbrace$

El siglo XIX se caracterizó por el desarrollo de la matemática por la matemática, sin estar necesariamente ligado a la solución de problemáticas de la vida cotidiana del momento. Emergieron conceptos como número racional, número irracional, número complejo, anillo, cuerpo, etcétera, pero nos centraremos en el concepto de número racional desde el punto de vista de la matemática escolar.

Los números racionales entregan la posibilidad de resolver todas las ecuaciones de la forma $ax+b=c$, con $a$, $b$ y $c$ enteros, permitiendo resolver todos los problemas que se modelan con estas ecuaciones. Además, están presentes en nuestra vida cotidiana en los distintos ámbitos del quehacer y representados de diversas maneras, por ejemplo, en el etiquetado de los alimentos, en los indicadores económicos, en las recetas médicas, etcétera.

El Conjunto de los Números Racionales

Un número racional es todo aquel que puede representarse como una fracción de números enteros. Simbólicamente, un número es racional si puede escribirse como:

$\dfrac{a}{b}, \; | \; \; a, b \in \mathbb{Z}, b \neq 0$

El conjunto de los números racionales se caracteriza por ser infinito, ordenado y denso. El símbolo $\mathbb{Q}$ denota al conjunto de los números racionales y proviene de la palabra inglesa quotient que significa cociente:

$\mathbb{Q} = \left\lbrace \dfrac{a}{b} \; \bigg/ \; a\in \mathbb{Z}, b \in \mathbb{Z}, b\neq 0 \right\rbrace$

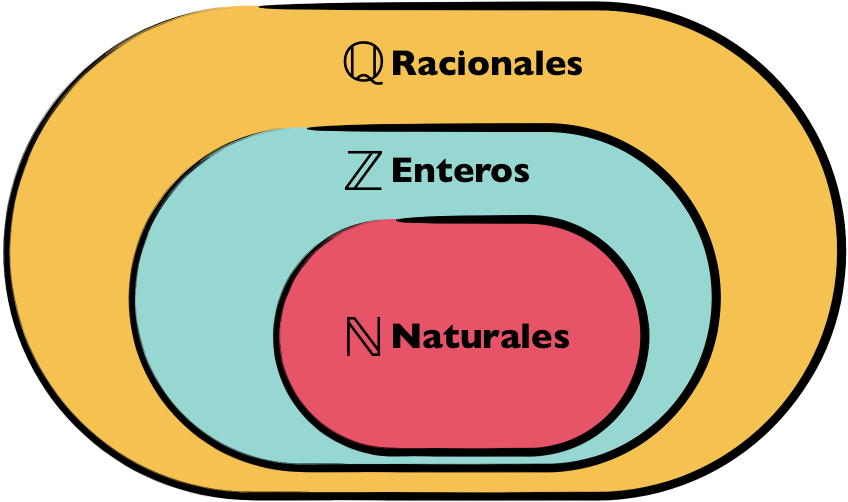
Subconjuntos de los Números Racionales

• El conjunto de los números naturales $\mathbb{N}$:

$\mathbb{N}=\{1, \; 2, \; 3, \; 4, \; 5, \; 6, \; 7, \dots\}$

• El conjunto de los números enteros $\mathbb{Z}$:

$\mathbb{Z}=\{\dots,-3, -2, -1, \; 0, \; 1, \; 2, \; 3, \dots\}$

Simbólicamente, esto se representa como $\mathbb{N}\subset \mathbb{Z}\subset \mathbb{Q}$.

Características de los Números Racionales

• Es un conjunto infinito ordenado.
• Existe neutro aditivo y es único (0).
• Todo número racional diferente de 0 tiene un inverso aditivo.
• Existe neutro multiplicativo y es único (1).
• Todo número racional diferente de 0 tiene un inverso multiplicativo.
• Entre dos números racionales siempre hay otro número racional.

Representación de los Números Racionales

Por definición, todo número racional puede ser representado como una fracción de la forma $\dfrac{a}{b}$, con $a$, $b$ números enteros y $b\neq 0$. La expresión $\dfrac{a}{b}$ es equivalente a la división $a:b$ y su cociente (el resultado de la división) puede ser un número entero o no.

Dentro del conjunto de números de la forma $\dfrac{a}{b}$, con $a$, $b$ números enteros y $b \neq 0$, pueden distinguirse estos subconjuntos de números positivos:

1. Fracciones propias: Son todas aquellas que tienen como cociente un número que está entre 0 y 1. En estas fracciones, el denominador es mayor que el numerador. Por ejemplo: $\dfrac{2}{3}$, $\dfrac{1}{10}$, $\dfrac{5}{7}$, etcétera.
2. Fracciones impropias: Son todas aquellas que tienen como cociente un número mayor que 1. En estas fracciones, el denominador es menor que el numerador. Por ejemplo: $\dfrac{3}{2}$, $\dfrac{15}{10}$, $\dfrac{8}{5}$, etcétera.

Como las fracciones impropias son mayores que 1, pueden escribirse como la suma de un número entero y una fracción propia. Esta forma se llama número mixto:

$1\dfrac{2}{3}=1+\dfrac{2}{3}$

$2\dfrac{1}{4}=2+\dfrac{1}{4}$

Para convertir una fracción impropia en un número mixto:

$$C\frac{a}{b} = \frac{b \cdot c+a}{b}$$

¿De dónde viene este algoritmo? Simplemente se está sumando un entero con una fracción. El procedimiento completo es:

$$C\dfrac{a}{b} = C + \dfrac{a}{b} = \dfrac{c}{1} + \dfrac{a}{b} = \dfrac{b\cdot c + a}{b}$$
3. Fracciones decimales: Son todas aquellas que pueden ser expresadas de la forma $\dfrac{n}{10^m}$, con $n$ número entero y $m$ número natural. Es decir, una fracción decimal tiene como denominador una potencia de 10. Son ejemplos de fracciones decimales $\dfrac{12}{10}$, $\dfrac{6}{100}$, $\dfrac{-1}{1000}$, etcétera.
4. Números decimales finitos: Son todos aquellos que provienen de fracciones que se pueden escribir como fracción decimal. Por ejemplo, 0.2, 0.43, 2.6, 15.808, etcétera.
5. Números decimales infinitos periódicos: Son todos aquellos que poseen una o más cifras decimales que se repiten sucesiva e infinitamente, formando el período. El período se puede escribir en forma abreviada colocando un trazo sobre las cifras decimales que se repiten. Por ejemplo, $0,\overline{3}$, $0,\overline{25}$, $12,\overline{4}$, etcétera.
6. Números decimales infinitos semiperiódicos: Son todos aquellos que poseen una o más cifras decimales antes del período. El período, al igual que en los decimales infinitos periódicos, corresponde a la o las cifras decimales que se repiten sucesiva e infinitamente, mientras que el anteperíodo corresponde a la o las cifras decimales que están antes del período. Por ejemplo, $0,0\overline{2}$, $5,4\overline{32}$, $11,67\overline{3}$, etcétera.

Mapa Conceptual

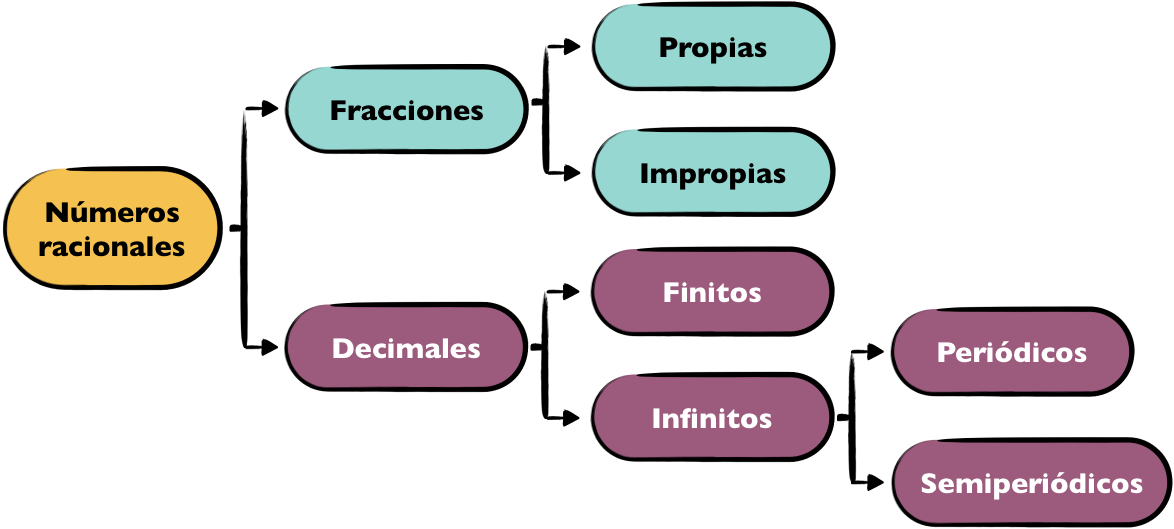
Números Racionales en la Recta Numérica

La recta numérica es un modelo del conjunto de los números reales, en este caso particular, del conjunto de los números racionales. Recuerda que un número racional es todo aquel que puede representarse como una fracción de números enteros.

La representación de los números racionales en la recta numérica permite visualizar la noción de orden, característica que no poseen otras representaciones gráficas de los elementos de este conjunto.

En términos generales, para representar números racionales en la recta numérica, se deben ubicar los números positivos a la derecha del cero y los números negativos a su izquierda. Al representar números negativos, será mayor aquel número que esté más cerca del cero y menor aquel que esté a mayor distancia del cero.

Números racionales en la recta numérica

La recta numérica es un modelo del conjunto de los números reales, en este caso particular, del conjunto de los números racionales. Recuerda que un número racional es todo aquel que puede representarse como una fracción de números enteros. Simbólicamente, un número es racional si puede escribirse como $\dfrac{a}{b}$, tal que $a$ y $b$ son números enteros y $b \neq 0$.

La representación de los números racionales en la recta numérica permite visualizar la noción de orden, característica que no poseen otras representaciones gráficas de los elementos de este conjunto.

La representación de un número en la recta numérica se apoya en un procedimiento de medida de longitudes mediante el cual es posible resaltar un punto y atribuirle una representación simbólica, por ejemplo, una fracción, un número decimal o un número mixto.

En términos generales, para representar números racionales en la recta numérica, se deben ubicar los números positivos a la derecha del cero y los números negativos a su izquierda. Al representar números negativos, será mayor aquel número que esté más cerca del cero y menor aquel que esté a mayor distancia del cero.

Representación de números fraccionarios en la recta numérica

Para representar números fraccionarios en la recta numérica, es recomendable determinar en cuántos tramos se debe dividir los segmentos que representan una unidad. En términos generales, se deben dividir los trazos unitarios según el denominador de la fracción y se debe ubicar la fracción tantos lugares desde el cero a la derecha o izquierda, según el signo de la fracción, como lo indique el numerador.

Por ejemplo, ¿cómo ubicar $\dfrac{1}{6}$ en la recta numérica? En primer lugar, como $\dfrac{1}{6}$ es una fracción propia, está entre $0$ y $1$.

El trazo unitario entre $0$ y $1$ se debe dividir en $6$ segmentos iguales porque el denominador es $6$.

Como el numerador de $\dfrac{1}{6}$ es $1$, la fracción se ubica un sexto a la derecha del $0$.

Pregunta:

De acuerdo a lo anterior, ¿qué número se ubica en $\bigstar$?

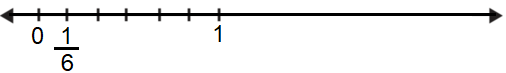
Ver solución

Como la fracción se ubica un sexto a la derecha de $0$, el número en $\bigstar$ es $\dfrac{1}{6}$.

Veamos otro ejemplo, ¿dónde se ubica $\dfrac{11}{6}$ en la recta numérica? En este caso, como $\dfrac{11}{6}$ es una fracción impropia, es mayor que $1$. Como el denominador es $6$, la fracción $\dfrac{11}{6}$ se ubica en $11$ sextos a la derecha del $0$.

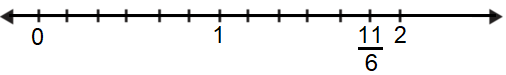
El procedimiento descrito permite ubicar cualquier número fraccionario en la recta numérica, positivo o negativo. Note que no necesariamente la recta numérica debe comenzar en $0$ cuando se trata de una fracción impropia, pero sí es necesario que se divida en partes iguales. Para determinar en qué número entero es conveniente que parta la recta numérica cuando se necesita ubicar una fracción impropia, es recomendable representar el número fraccionario como número mixto. Por ejemplo:

¿Dónde se ubica la fracción $\dfrac{17}{3}$? Como se trata de una fracción impropia, es mayor que $1$, pero ¿de qué entero está más cercano?

La fracción $\dfrac{17}{3} = 5 + \dfrac{2}{3} = 5 \dfrac{2}{3}$, por lo que está dos tercios a la derecha de $5$.

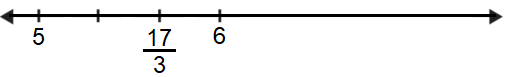
Representación de números decimales en la recta numérica

Para representar números decimales en la recta numérica, es recomendable determinar en cuántos tramos se debe dividir los segmentos que representan una unidad. Comencemos estudiando cómo ubicar números decimales finitos en la recta numérica.

Por ejemplo, ¿cómo ubicar $0,4$ en la recta numérica? La parte entera de $0,4$ es $0$, por lo que este decimal es mayor que $0$ y menor que $1$. Antes de comenzar a trabajar con la recta numérica, recuerda cómo se escribe $0,4$ con palabras: “cuatro décimos”. Una décima corresponde a $1$ de las $10$ partes iguales que dividen la unidad. Así, $0,4 = \dfrac{4}{10}$, por lo que el trazo unitario entre $0$ y $1$ se debe dividir en $10$ segmentos iguales.

Como el numerador de $\dfrac{4}{10}$ es $4$, la fracción se ubica cuatro décimos a la derecha del $0$.

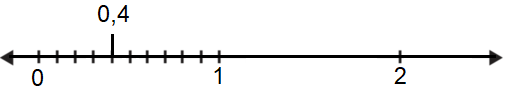
En términos generales, los decimales finitos pueden ser representados como fracción decimal, por lo que para ser ubicados en la recta numérica basta con escribirlos como fracción y usar el método descrito anteriormente.

¿Cómo ubicar números decimales infinitos periódicos y semiperiódicos en la recta numérica? Recuerda que estos decimales son números racionales, por lo que es posible representarlos como fracción de números enteros. Por ejemplo, ¿dónde se ubica $1,\overline{2}$? Como número periódico, $1,\overline{2} = \dfrac{12 - 1}{9} = \dfrac{11}{9} = 1 + \dfrac{2}{9} = 1 \dfrac{2}{9}$.

El número $1 \dfrac{2}{9}$ se ubica dos novenos a la derecha del $1$.

La tarea de ubicar números racionales en la recta numérica permite elaborar distintas situaciones y problemáticas. Por ejemplo, ubicar en la recta numérica cinco números que se encuentren entre $0,01$ y $0,02$. Una forma es ubicar $0,01$ y $0,02$ en los extremos de la recta numérica y dividir el segmento entre ambos en $10$ partes iguales. Cada parte representa $0,001 = \dfrac{1}{1000}$.

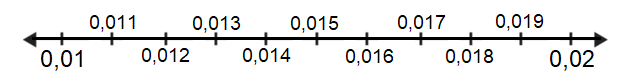
Orden, comparación y operatoria de racionales

Relaciones de orden

• Positivo: $a$ es positivo si $a > 0$.
• Negativo: $a$ es negativo si $a < 0$.
• Mayor que: $a$ es mayor que $b$ si $a - b > 0$.
• Entre: Si $a < b$ y $c \in \mathbb{Q}$, decimos que $c$ está entre $a$ y $b$ si $a < c < b$.

Para cualesquiera $a,b \in \mathbb{Q}$ se cumple una y solo una de las siguientes afirmaciones:

$$\begin{aligned} a &< b,\\ a &= b,\\ a &> b. \end{aligned}$$

A esto se le denomina tricotomía.

Operatoria

Para $a,b,c,d\in \mathbb{Z}$ con $b,c,d \neq 0$ se cumplen:

• $\dfrac{a}{c} \pm \dfrac{b}{c} = \dfrac{a \pm b}{c}$
• $\dfrac{a}{b} \pm \dfrac{c}{d} = \dfrac{a\cdot d \pm b\cdot c}{b\cdot d}$
• $\dfrac{a}{b} \cdot \dfrac{c}{d} = \dfrac{a\cdot c}{b\cdot d}$
• $\dfrac{a}{b} \div \dfrac{c}{d} = \dfrac{a}{b} \cdot \dfrac{d}{c}$

Dividir es lo mismo que multiplicar por el inverso multiplicativo (recíproco) del divisor.

Fracciones equivalentes: Dos fracciones que representan el mismo valor numérico se denominan fracciones equivalentes.

Amplificación

Amplificación es multiplicar numerador y denominador de una fracción por la misma cantidad (≠0) para obtener una fracción equivalente.

Por ejemplo:

$$\frac{4}{11} = \frac{4 \cdot 2}{11 \cdot 2} = \frac{8}{22}.$$

Simplificación

Simplificación es dividir numerador y denominador de una fracción por un mismo divisor para obtener una fracción equivalente en forma reducida.

Por ejemplo:

$$\frac{12}{8} = \frac{12 \div 4}{8 \div 4} = \frac{3}{2}.$$

Comparar racionales

Podemos comparar fracciones mediante diferentes métodos. A continuación, algunos de ellos.

Multiplicación cruzada

Para fracciones positivas $\frac{a}{b}$ y $\frac{c}{d}$:

• $\displaystyle \frac{a}{b} > \frac{c}{d}$ si y solo si $a \cdot d > b \cdot c$.
• $\displaystyle \frac{a}{b} = \frac{c}{d}$ si y solo si $a \cdot d = b \cdot c$.
• $\displaystyle \frac{a}{b} < \frac{c}{d}$ si y solo si $a \cdot d < b \cdot c$.

Igualando denominadores

Amplifica ambas fracciones para tener un mismo denominador, luego compara numeradores. Por ejemplo, para comparar $\frac{11}{13}$ y $\frac{4}{5}$, las amplificamos a denominador $65$:

$$\frac{11}{13} = \frac{11 \cdot 5}{13 \cdot 5} = \frac{55}{65},\quad \frac{4}{5} = \frac{4 \cdot 13}{5 \cdot 13} = \frac{52}{65}.$$

Como $55 > 52$, entonces $\frac{11}{13} > \frac{4}{5}$.

Igualando numeradores

Amplifica ambas fracciones para tener un mismo numerador, luego compara denominadores (aplicable solo a denominadores positivos). Siguiendo el ejemplo anterior:

$$\frac{11}{13} = \frac{11 \cdot 4}{13 \cdot 4} = \frac{44}{52},\quad \frac{4}{5} = \frac{4 \cdot 11}{5 \cdot 11} = \frac{44}{55}.$$

Dado que $52 < 55$, se cumple $\frac{44}{52} > \frac{44}{55}$, luego $\frac{11}{13} > \frac{4}{5}$.

Representación decimal

Recuerda que un número racional es todo aquel que puede representarse como una fracción de números enteros, con denominador distinto de $0$. Los números decimales infinitos periódicos y semiperiódicos son números racionales, es decir, pueden representarse como fracción de números enteros.

En este documento se explicará qué son los números decimales infinitos periódicos y semiperiódicos, cómo representarlos como fracción y se entregará la justificación del procedimiento de transformación, de manera que no se presente como una receta.

Números decimales infinitos periódicos

Los números decimales infinitos periódicos son aquellos que poseen una o más cifras decimales que se repiten infinitamente. El período puede abreviarse con un trazo sobre las cifras que se repiten.

• $0,3333\dots = 0,\overline{3}$ (período $3$).
• $5,1212\dots = 5,\overline{12}$ (período $12$).
• $10,931\dots = 10,\overline{931}$ (período $931$).

Para convertir un decimal periódico a fracción, sigue estos pasos:

tip

1. Escribe en el numerador el número decimal sin la coma, y réstale la parte entera.
2. En el denominador, coloca tantos nueves como cifras tenga el período.

Ejemplo 1

Convertir $1,\overline{7}$ en fracción:

$$\frac{17 - 1}{9} = \frac{16}{9}$$

Comprobación:

$$\begin{aligned} x &= 1,\overline{7},\\ 10x &= 17,\overline{7},\\ 10x - x &= 17,\overline{7} - 1,\overline{7} = 16,\\ 9x &= 16,\quad x = \frac{16}{9}. \end{aligned}$$

Convertir $2,\overline{104}$ en fracción:

$$\frac{2104 - 2}{999} = \frac{2102}{999}$$

Comprobación:

$$\begin{aligned} y &= 2,\overline{104},\\ 1000y &= 2104,\overline{104},\\ 1000y - y &= 2104,\overline{104} - 2,\overline{104} = 2102,\\ 999y &= 2102,\quad y = \frac{2102}{999}. \end{aligned}$$

Números decimales infinitos semiperiódicos

Los números decimales infinitos semiperiódicos tienen un anteperíodo (cifras antes del período) y un período que se repite infinitamente.

• $0,5333\dots = 0,5\overline{3}$ (anteperíodo $5$, período $3$).
• $7,41555\dots = 7,41\overline{5}$ (anteperíodo $41$, período $5$).
• $26,23479479479\dots = 26,23\overline{479}$ (anteperíodo $23$, período $479$).

Para convertir un decimal semiperiódico a fracción:

tip

1. En el numerador, escribe el decimal sin la coma y réstale todos los dígitos antes del período.
2. En el denominador, coloca tantos nueves como cifras tenga el período, seguidos de tantos ceros como cifras tenga el anteperíodo.

Ejemplo 1

Convertir $0,4\overline{1}$:

$$\frac{41 - 4}{90} = \frac{37}{90}$$

Comprobación:

$$\begin{aligned} z &= 0,4\overline{1},\\ 10z &= 4,1\overline{1},\\ 100z &= 41,\overline{1},\\ 100z - 10z &= 41,\overline{1} - 4,\overline{1} = 37,\\ 90z &= 37,\quad z = \frac{37}{90}. \end{aligned}$$

Ejemplo 2

Convertir $5,12\overline{1}$:

$$\frac{5121 - 512}{900} = \frac{4609}{900}$$

Comprobación:

$$\begin{aligned} w &= 5,12\overline{1},\\ 100w &= 512,\overline{1},\\ 1000w &= 5121,\overline{1},\\ 1000w - 100w &= 5121,\overline{1} - 512,\overline{1} = 4609,\\ 900w &= 4609,\quad w = \frac{4609}{900}. \end{aligned}$$

Clausura del conjunto de los números racionales

En el conjunto de los números racionales, las operaciones de adición, multiplicación, sustracción y división (con divisor distinto de cero) cumplen con la propiedad de clausura; es decir, al operar con números racionales siempre se obtiene otro número racional.

Pregunta:

¿El operador $p \triangle q = p - q \cdot p + q$ cumple con la propiedad de clausura?

Dado que $p$ y $q$ son números racionales y la adición, multiplicación y sustracción en $\mathbb{Q}$ cumplen la propiedad de clausura, se concluye que el resultado de $p \triangle q$ también es racional, por lo que $p \triangle q$ cumple la propiedad de clausura.

Densidad del conjunto de los números racionales

El conjunto de los números racionales es denso, es decir, entre dos números racionales siempre existe otro número racional. Por lo tanto, entre cualquier par $a,b\in\mathbb{Q}$ se pueden encontrar infinitos números racionales.

Por ejemplo, entre $0,01$ y $0,02$ encontramos nueve números racionales, pero podemos hallar el promedio entre cualquiera de ellos para ubicar uno nuevo:

$$\frac{0,01 + 0,011}{2} = \frac{0,021}{2} = 0,0105$$

Este procedimiento puede iterarse indefinidamente, demostrando que siempre existen más números racionales entre dos dados.